题目内容
在研究反比例函数图象与性质时,由于计算粗心,小明误认为(-2,3)、(2,-3)、(-2,-3)、(3,-2)、( ,4)五个点在同一个反比例函数的图象上,后来经检查发现其中有一个点不在,这个点是( )
,4)五个点在同一个反比例函数的图象上,后来经检查发现其中有一个点不在,这个点是( )A.(2,-3)
B.(-2,3)
C.(-2,-3)
D.(
 ,4)
,4)
【答案】分析:在同一反比例函数的图象上,k的值就相等.由题意得:k=xy,横纵坐标相乘得比例系数.只需把所给点的横纵坐标相乘,结果相等的,就在此函数图象上;反之,就不在.
解答:解:A、2×(-3)=-6;
B、(-2)×3=-6;
C、(-2)×(-3)=6;
D、(- )×4=-6.
)×4=-6.
故选C.
点评:本题主要考查反比例函数图象上点的坐标特征,所有在反比例函数y= 图象上的点的横纵坐标的积都等于其比例系数k.
图象上的点的横纵坐标的积都等于其比例系数k.
解答:解:A、2×(-3)=-6;
B、(-2)×3=-6;
C、(-2)×(-3)=6;
D、(-
 )×4=-6.
)×4=-6.故选C.
点评:本题主要考查反比例函数图象上点的坐标特征,所有在反比例函数y=
 图象上的点的横纵坐标的积都等于其比例系数k.
图象上的点的横纵坐标的积都等于其比例系数k. 
练习册系列答案
相关题目
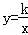 上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.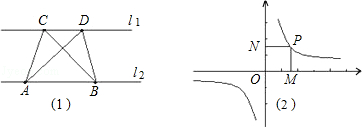

 上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.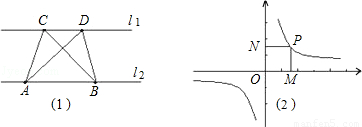
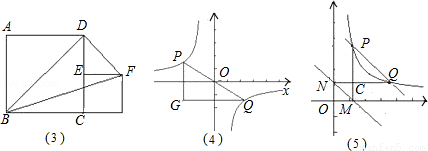
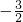 ,4)五个点在同一个反比例函数的图象上,后来经检查发现其中有一个点不在,这个点是
,4)五个点在同一个反比例函数的图象上,后来经检查发现其中有一个点不在,这个点是