题目内容
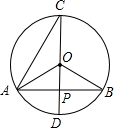如图，在⊙O中，P是弦AB的中点，CD是过点P的直径，则下列结论中不正确的是（ ）| A、AB⊥CD | ||||
| B、∠AOB=4∠ACD | ||||
C、
| ||||
| D、PO=PD |
分析：根据垂径定理及圆周角定理可直接解答．
解答：解：∵P是弦AB的中点，CD是过点P的直径，
∴AB⊥CD，
=
，△AOB是等腰三角形，
∴∠AOB=2∠AOP，
∵∠AOP=2∠ACD，
∴∠AOB=2∠AOP=2×2∠ACD=4∠ACD．
故选D．
∴AB⊥CD，
 |
| AD |
|
| BD |
∴∠AOB=2∠AOP，
∵∠AOP=2∠ACD，
∴∠AOB=2∠AOP=2×2∠ACD=4∠ACD．
故选D．
点评：本题主要利用平分弦（不是直径）的直径垂直于这条弦，并且平分这条弦所对的两段弧的性质选择．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
7、如图，在△ABC中，BD是∠ABC的平分线，DE∥BC，交AB与点E，∠A=60°，∠BDC=105°，则∠BDE=（ ）
如图，在?ABCD中，E是BC的中点，且∠AEC=∠DCE，下列结论中正确的有（ ）
已知：如图，在△ABC中，AD是它的角平分线，且EB=FC，DE⊥AB，DF⊥AC，垂足分别为E，F．求证：BD=CD．
如图，在△ABC中，AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，试猜想EF与AD之间有什么关系？并证明你的猜想．
已知：如图，在△ABC中，D是BC边的中点，E是AD的中点，连接BE并延长到点F，使EF=BE，连接AF、CF．