题目内容
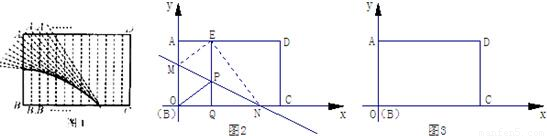
问题背景:在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息如图1:甲组:测得一根直立于平地,长为80cm的竹竿的影长为60cm;
如图2:乙组:测得学校旗杆的影长为900cm;
如图3:丙组:测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为350cm,影长为300cm.
解决问题:
(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度?
(2)如图3,设太阳光线MH与⊙O相切于点M,请根据甲、丙两组得到的信息,求景灯灯罩的半径?
分析:(1)根据同一时刻物高与影长成正比即可求出旗杆的高度;
(2)先根据同一时刻物高与影长成正比求出NG的长,再连接OM,由切线的性质可知OM⊥NH,进而可得出△NMO∽△NGH,再根据其对应边成比例列出比例式,然后用半径表示出ON,进行计算即可求出OM的长.
(2)先根据同一时刻物高与影长成正比求出NG的长,再连接OM,由切线的性质可知OM⊥NH,进而可得出△NMO∽△NGH,再根据其对应边成比例列出比例式,然后用半径表示出ON,进行计算即可求出OM的长.
解答: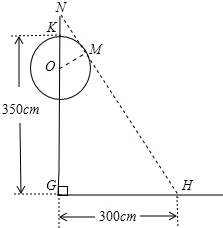 解:(1)∵同一时刻物高与影长成正比,
解:(1)∵同一时刻物高与影长成正比,
∴
=
,
即
=
,
解得DE=1200cm;
(2)连接OM,设OM=r,
∵同一时刻物高与影长成正比,
∴
=
,
即
=
,
解得NG=400cm,
在Rt△NGH中,NH=
=
=500cm,
设⊙O的半径为r,
∵MH与⊙O相切于点M,
∴OM⊥NH,
∴∠NMO=∠NGH=90°,
又∵∠ONM=∠GNH,
∴△NMO∽△NGH,
∴
=
,
即
=
,
又∵NO=NK+KO=(NG-KG)+KO=400-350+r=50+r,
∴500r=300(50+r),
解得r=75cm.
故景灯灯罩的半径是75cm.
 解:(1)∵同一时刻物高与影长成正比,
解:(1)∵同一时刻物高与影长成正比,∴
| AB |
| AC |
| DE |
| DF |
即
| 80 |
| 60 |
| DE |
| 900 |
解得DE=1200cm;
(2)连接OM,设OM=r,
∵同一时刻物高与影长成正比,
∴
| AB |
| AC |
| NG |
| GH |
即
| 80 |
| 60 |
| NG |
| 300 |
解得NG=400cm,
在Rt△NGH中,NH=
| NG2+HG2 |
| 4002+3002 |
设⊙O的半径为r,
∵MH与⊙O相切于点M,
∴OM⊥NH,
∴∠NMO=∠NGH=90°,
又∵∠ONM=∠GNH,
∴△NMO∽△NGH,
∴
| OM |
| GH |
| NO |
| NH |
即
| r |
| 300 |
| NO |
| 500 |
又∵NO=NK+KO=(NG-KG)+KO=400-350+r=50+r,
∴500r=300(50+r),
解得r=75cm.
故景灯灯罩的半径是75cm.
点评:本题考查了把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求解,体现了转化的思想.此题的文字叙述比较多,解题时要认真分析题意.

练习册系列答案
相关题目
 ,若存在,写出点K的坐标;若不存在,请说明理由.
,若存在,写出点K的坐标;若不存在,请说明理由.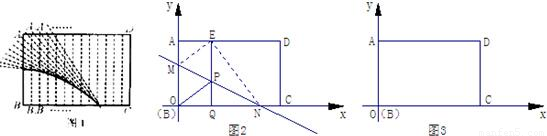
 ,若存在,写出点K的坐标;若不存在,请说明理由.
,若存在,写出点K的坐标;若不存在,请说明理由.