题目内容
求证：方程x2-（k+6）x+4（k-3）=0一定有两个不相等的实数根．
证明：∵△=（k+6）2-4×1×4（k-3）=（k-2）2+80，
而（k-2）2≥0，
∴（k-2）2+80＞0，
即△＞0，
所以不论k取什么实数，方程x2-（k+6）x+4（k-3）=0一定有两个不相等的实数根．
分析：要证明不论k取什么实数，方程x2-（k+6）x+4（k-3）=0一定有两个不相等的实数根，即证明△＞0即可．
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）根的判别式△=b2-4ac．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．也考查了代数式的变形能力．
而（k-2）2≥0，
∴（k-2）2+80＞0，
即△＞0，
所以不论k取什么实数，方程x2-（k+6）x+4（k-3）=0一定有两个不相等的实数根．
分析：要证明不论k取什么实数，方程x2-（k+6）x+4（k-3）=0一定有两个不相等的实数根，即证明△＞0即可．
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）根的判别式△=b2-4ac．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．也考查了代数式的变形能力．
练习册系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
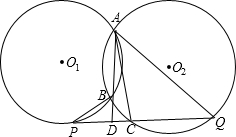求S△ADC：S△ACQ的值．