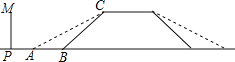
题目内容
【题目】已知△ABC中,∠ACB=90°,CD、CE分别是中线和角平分线,当∠A= °时,△CDE是等腰三角形.
【答案】15或75.
【解析】
试题分析:有两种情况:①中线CD在角平分线CE的左边,由直角三角形斜边中线定理可以知道△BCD是等腰三角形,△CDE要是等腰三角形只有一种情况,即CE=DE,∠DCE=∠CDE,由外角定理可以知道∠CDE=∠B+∠BCD=2∠BCD,又因为∠CDE=∠DCE,且∠DCE+∠BCD=45°,所以3∠BCD=3∠B=45°,∠B=15°,∠A=90°-∠B=75°;
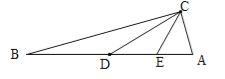
②中线CD在角平分线CE的右边,由直角三角形斜边中线定理可以知道△ACD是等腰三角形,△CDE要是等腰三角形只有一种情况,即CE=DE,∠DCE=∠CDE,由外角定理可以知道∠CDE=∠A+∠ACD=2∠ACD,又因为∠CDE=∠DCE,且∠DCE+∠ACD=45°,所以3∠ACD=3∠A=45°,∠A=15°;故答案为:15或75.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目