题目内容
以正方形ABCD的BC边为直径作半圆O，过点D作直线切半圆于点F，交AB边于点E．则三角形ADE和直角梯形EBCD周长之比为（ ）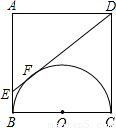
A．3：4
B．4：5
C．5：6
D．6：7
【答案】分析：设EF=x，DF=y，在△ADE中根据勾股定理可得列方程，从而得到三角形ADE的周长和直角梯形EBCD周长，从而可求得两者周长之比．
解答：解：根据切线长定理得，BE=EF，DF=DC=AD=AB=BC．
设EF=x，DF=y，
则在直角△AED中，AE=y-x，AD=CD=y，DE=x+y．
根据勾股定理可得：
（y-x）2+y2=（x+y）2，
∴y=4x，
∴三角形ADE的周长为12x，直角梯形EBCD周长为14x，
∴两者周长之比为12x：14x=6：7．
故选D．
点评：此题考查圆的切线长定理，正方形的性质和勾股定理等知识，解答本题关键是运用切线长定理得出EB=EF，DF=DC，从而求解．
解答：解：根据切线长定理得，BE=EF，DF=DC=AD=AB=BC．
设EF=x，DF=y，
则在直角△AED中，AE=y-x，AD=CD=y，DE=x+y．
根据勾股定理可得：
（y-x）2+y2=（x+y）2，
∴y=4x，
∴三角形ADE的周长为12x，直角梯形EBCD周长为14x，
∴两者周长之比为12x：14x=6：7．
故选D．
点评：此题考查圆的切线长定理，正方形的性质和勾股定理等知识，解答本题关键是运用切线长定理得出EB=EF，DF=DC，从而求解．
练习册系列答案
阅读快车系列答案
相关题目
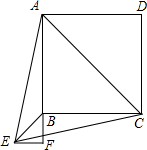如图，已知：△AEC是以正方形ABCD的对角线为边的等边三角形，EF⊥AB，交AB延长线于F，则∠BEF度数为
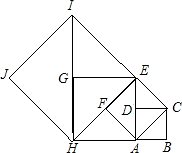如图所示，如果以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以AE为边作第三个正方形AEGM，…已知正方形ABCD的面积S1=1，按上述方法所作的正方形的面积依次为S2，S3，…Sn（n为正整数），那么第8个正方形面积S8=
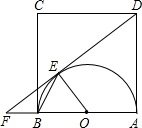B的延长线于点F，BF=4．
已知：如图，以正方形ABCD的对角线为边作菱形AEFC，B在FE的延长线上．