题目内容
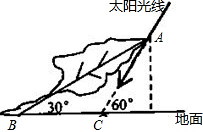 如图,太阳光线与地面成60°角,一棵倾斜的大树AB与地面成30°角,这时测得大树在地面的影长BC为10m,则大树的长为( )m.
如图,太阳光线与地面成60°角,一棵倾斜的大树AB与地面成30°角,这时测得大树在地面的影长BC为10m,则大树的长为( )m.A、5
| ||
B、10
| ||
C、15
| ||
D、20
|
分析:如图,即求AC的长,因为60°的角时△ABC的一个外角,且∠C为30°已知,所以根据三角形外角和可知∠CAB=30°,即AC=BC=10m,从而利用△ABD求出BD的长,即可求出CD,利用30°角的余弦值,进而求出AC.
解答: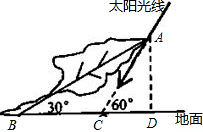 解:如图,作AD⊥CD于D点.
解:如图,作AD⊥CD于D点.
因为∠B=30°,∠ACD=60°,
且∠ACD=∠B+∠CAB,
∴∠CAB=30°.
∴BC=AC=10m,
在Rt△ACD中,CD=AC•cos60°=10×0.5=5m,
∴BD=15.
∴在Rt△ABD中,
AB=BD÷cos30°=15÷
=10
m.
故选B.
 解:如图,作AD⊥CD于D点.
解:如图,作AD⊥CD于D点.因为∠B=30°,∠ACD=60°,
且∠ACD=∠B+∠CAB,
∴∠CAB=30°.
∴BC=AC=10m,
在Rt△ACD中,CD=AC•cos60°=10×0.5=5m,
∴BD=15.
∴在Rt△ABD中,
AB=BD÷cos30°=15÷
| ||
| 2 |
| 3 |
故选B.
点评:本题考查锐角三角函数的运用,构造所求线段所在的直角三角形是难点.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
 如图,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影长约为10m,则大树的长约为
如图,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影长约为10m,则大树的长约为 如图,太阳光线与地面成60°角,一棵倾斜的大树在地面上的影长约为10米,则大树的长为
如图,太阳光线与地面成60°角,一棵倾斜的大树在地面上的影长约为10米,则大树的长为 如图,太阳光线与地面成60°角,一颗倾斜的大树与地面成30°角,这时测得大树在地面上的树影长为8 m,则大树的长为
如图,太阳光线与地面成60°角,一颗倾斜的大树与地面成30°角,这时测得大树在地面上的树影长为8 m,则大树的长为 (2010•李沧区二模)如图,太阳光线与地面成63°角,一棵倾斜的大树(AB)与地面成34°角,这时测得大树在地面的影长约为10米.求AB的长.(结果保留两个有效数字)
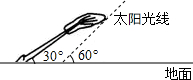
(2010•李沧区二模)如图,太阳光线与地面成63°角,一棵倾斜的大树(AB)与地面成34°角,这时测得大树在地面的影长约为10米.求AB的长.(结果保留两个有效数字) 如图,太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影长是10
如图,太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影长是10