题目内容
如图所示，在△ABC中，∠BAC=135°，EF、GH分别是AB、AC两边的垂直平分线，与BC边交于点E、G，求∠EAG的度数．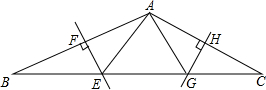
∵EF、GH分别是AB、AC两边的垂直平分线，
∴AE=BE，AG=CG，
∴∠BAE=∠B，∠CAG=∠C，
∵∠BAC=135°，
∴∠B+∠C=180°-∠BAC=45°，
∴∠BAE+∠CAG=45°，
∴∠EAG=∠BAC-（∠BAE+∠CAG）=135°-45°=90°．
∴AE=BE，AG=CG，
∴∠BAE=∠B，∠CAG=∠C，
∵∠BAC=135°，
∴∠B+∠C=180°-∠BAC=45°，
∴∠BAE+∠CAG=45°，
∴∠EAG=∠BAC-（∠BAE+∠CAG）=135°-45°=90°．
练习册系列答案
名校课堂系列答案
相关题目
