题目内容
(本小题满分7分)
已知:关于 的一元二次方程
的一元二次方程 .
.
(1)若方程有两个不相等的实数根,求 的取值范围;
的取值范围;
(2)在(1)的条件下,求证:无论 取何值,抛物线y=
取何值,抛物线y= 总过
总过 轴上的一个固定点;
轴上的一个固定点;
(3)若 为正整数,且关于
为正整数,且关于 的一元二次方程
的一元二次方程 有两个不相等的整数根,把抛物线y=
有两个不相等的整数根,把抛物线y= 向右平移4个单位长度,求平移后的抛物线的解析式.
向右平移4个单位长度,求平移后的抛物线的解析式.
【答案】
解:(1)∵关于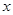 的一元二次方程
的一元二次方程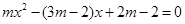 有两个不相等的实数根
有两个不相等的实数根
∴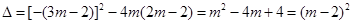 >0 ---------- 1分
>0 ---------- 1分
∴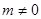 且m≠2
------------------------------------2分
且m≠2
------------------------------------2分
(2)证明:令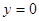 得,
得,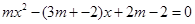
∴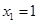 ,
,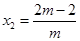 ------------------------------4分
------------------------------4分
∴抛物线与x轴的交点坐标为(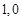 ),(
),( )
)
∴无论m取何值,抛物线y=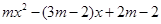 总过x轴上的定点(
总过x轴上的定点(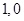 )---5分
)---5分
(3)∵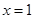 是整数 ∴只需
是整数 ∴只需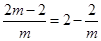 是整数.
是整数.
∵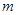 是正整数,且
是正整数,且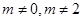
∴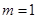 .
------------------------------- 6分
.
------------------------------- 6分
当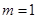 时,抛物线为
时,抛物线为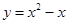
把它的图象向右平移4个单位长度,得到的抛物线解析式为
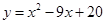 ---------------------------7分
---------------------------7分
【解析】略

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 (本小题满分6分,请在下列两个小题中,任选其一完成即可)
(本小题满分6分,请在下列两个小题中,任选其一完成即可)

 ,并
,并 来.
来.
