题目内容
【题目】给出下列四个命题:
①如果某圆锥的侧面展开图是半圆,则其轴截面一定是等边三角形;
②若点A在直线y=2x﹣3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
③半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的点共有四个;
④若A(a,m)、B(a﹣1,n)(a>0)在反比例函y= ![]() 的图象上,则m<n.
的图象上,则m<n.
其中,正确命题的个数是( )
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解:根据对称性可知.
①如果某圆锥的侧面展开图是半圆,则其轴截面一定是等边三角形,正确;
②如果点A到两坐标轴的距离相等,那么点A是y=x与y=2x﹣3的交点,是(3,3),在第一象限,或点A是y=﹣x与y=2x﹣3的交点,是(1,﹣1),在第四象限.则点A在第一或第四象限是正确的;
③半径为5的圆中,弦AB=8,则弦心距是3,圆周上到直线AB的距离为2的点是平行于AB,弦心距是2的弦与圆的交点.再加上垂直于弦AB的半径与圆的交点共3个,故其错误;
④若A(a,m)、B(a﹣1,n)(a>0)在反比例函y= ![]() 的图象上,而a与a﹣1的不能确定是否同号,即A,B不能确定是否在同一象限内,故m与n的大小关系无法确定.故错误.
的图象上,而a与a﹣1的不能确定是否同号,即A,B不能确定是否在同一象限内,故m与n的大小关系无法确定.故错误.
故选:B.
【考点精析】认真审题,首先需要了解由三视图判断几何体(在三视图中,通过主视图、俯视图可以确定组合图形的列数;通过俯视图、左视图可以确定组合图形的行数;通过主视图、左视图可以确定行与列中的最高层数).

 探究与巩固河南科学技术出版社系列答案
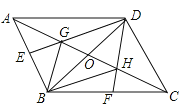
探究与巩固河南科学技术出版社系列答案【题目】如图,已知G、H是△ABC的边AC的三等分点,GE∥BH,交AB于点E,HF∥BG交BC于点F,延长EG、FH交于点D,连接AD、DC,设AC和BD交于点O,求证:四边形ABCD是平行四边形.
【题目】阅读理解:德国著名数学家高斯被认为是历史上最重要的数学家之一,并有"数学王子"的美誉.高斯从小就善于观察和思考.在他读小学时候就能在课堂上快速的计算出![]() ,今天我们可以将高斯的做法归纳如下:
,今天我们可以将高斯的做法归纳如下:
令![]() ①
①
![]() ②
②
(右边相加100+1=2+99=3+98=…..=100+1共100组)
①+②:有2S=101x100 解得:![]()
(1)请参照以上做法,回答,3+5+7+9+…..+97= ;
请尝试解决下列问题:
如下图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.

(2)填写下表:
层数 | 1 | 2 | 3 | 4 |
该层对应的点数 | 1 | 6 | 12 | 18 |
所有层的总点数的和 | 1 | 7 | 19 |
①写出第n层所对应的点数;(n≥2)
②如果某一层共96个点,求它是第几层;
③写出n层的六边形点阵的总点数.