题目内容
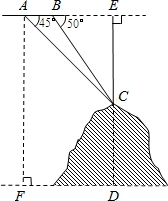（2013•南通二模）如图，某飞机于空中探测某座山的高度，在点A处飞机的飞行高度是AF=3700米，从飞机上观测山顶目标C的俯角是45°，飞机继续以相同的高度飞行300米到B处，此时观测目标C的俯角是50°，求这座山的高度CD．（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.20）．
分析：设EC=x，则在RT△BCE中，可表示出BE，在Rt△ACE中，可表示出AE，继而根据AB+BE=AE，可得出方程，解出即可得出答案．
解答：解：设EC=x，
在Rt△BCE中，tan∠EBC=
，
则BE=
=
x，
在Rt△ACE中，tan∠EAC=
，
则AE=
=x，
∵AB+BE=AE，
∴300+
x=x，
解得：x=1800，
胡可的山高CD=DE-EC=3700-1800=1900（米）．
答：这座山的高度是1900米．
在Rt△BCE中，tan∠EBC=
| EC |
| BE |
则BE=
| EC |
| tan∠EBC |
| 5 |
| 6 |
在Rt△ACE中，tan∠EAC=
| EC |
| AE |
则AE=
| EC |
| tan∠EAC |
∵AB+BE=AE，
∴300+
| 5 |
| 6 |
解得：x=1800，
胡可的山高CD=DE-EC=3700-1800=1900（米）．
答：这座山的高度是1900米．
点评：此题考查了解直角三角形的应用，解答本题的关键是两次利用三角函数的知识，求出BE及AE的表达式，属于基础题，要能将实际问题转化为数学计算．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
（2013•南通二模）如图，A、B、C、D是⊙O上的四点，OA⊥BC，∠AOB=50°，则∠ADC的度数是（ ）