题目内容
【题目】如图,已知AB=10,P是线段AB上的任意一点,在AB的同侧分别以AP、PB为边作等边三角形APC和等边三角形PBD,连结CD.
(1)当AP=6时,求CD的长;
(2)当AP为多少时,CD的值最小,最小值是多少?

【答案】(1)2![]() ;(2)当AP=5时,CD的长度最小,最小值是5.
;(2)当AP=5时,CD的长度最小,最小值是5.
【解析】
(1)如图,过C作CE⊥AB于E,过D作DF⊥PB于F,过D作DG⊥CE于G.即可得四边形DFEG为矩形.根据等边三角形的性质及矩形的性质求得EF=5,CG=![]() ,再利用勾股定理求得CD的长即可;(2)在(1)的基础上可得CD=
,再利用勾股定理求得CD的长即可;(2)在(1)的基础上可得CD=![]() ,当CG=0时,CD有最小值,由此求得CD的长即可.
,当CG=0时,CD有最小值,由此求得CD的长即可.
(1)如图,过C作CE⊥AB于E,过D作DF⊥PB于F,过D作DG⊥CE于G.即可得四边形DFEG为矩形.
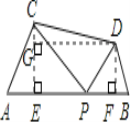
∵AB=10,AP=6,
∴PB=4,
∵△APC和△PBD是等边三角形,CE⊥AB , DF⊥PB,
∴EP=![]() AP=3,PF=
AP=3,PF=![]() PB=2,
PB=2,
∴EF=EP+FP=5.
在Rt△DPF中,DP=4,PF=2,
由勾股定理求得DF=![]() .
.
在Rt△CEP中,PC=6,PE=3,
由勾股定理求得CE=![]() .
.
由矩形的性质可得,DG=EF=5,EG=DF,
∴CG=![]() .
.
在Rt△CGD中,DG=5,CG=![]() ,由勾股定理求得CD=2
,由勾股定理求得CD=2![]() ;
;
(2)如图, 由(1)得,DG=EF=![]() AB=5,CD≥DG,
AB=5,CD≥DG,

∴CD=![]() ,故CG=0时,CD有最小值,
,故CG=0时,CD有最小值,
当P为AB中点时,有CD=DG=5,
所以CD长度的最小值是5.

练习册系列答案
相关题目