题目内容
 如图,OC为半径,AB为弦,OC⊥AB,垂足为D,OC=12cm,CD=6cm.则S弓形ACB=________.
如图,OC为半径,AB为弦,OC⊥AB,垂足为D,OC=12cm,CD=6cm.则S弓形ACB=________.
(48π-36 )cm2
)cm2
分析:根据垂径定理以及勾股定理得出AD的长以及利用锐角三角函数关系求出∠DOA=60°进而利用扇形面积公式和三角形面积公式求出即可.
解答: 解:连接BO,
解:连接BO,
∵OC⊥AB,垂足为D,OC=12cm,CD=6cm,
∴AO=12cm,AD= =6
=6 cm,
cm,
cos∠DOA= =
=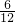 =
= ,
,
∴AB=12 cm,
cm,
∴∠DOA=60°,
∴∠AOB=120°,
∴S扇形AOB-S△AOB= -
- ×6×12
×6×12 =(48π-36
=(48π-36 )cm2,
)cm2,
故答案为:(48π-36 )cm2.
)cm2.
点评:此题主要考查了扇形的面积计算和垂径定理的应用,根据已知得出∠AOB的度数是解题关键.
 )cm2
)cm2分析:根据垂径定理以及勾股定理得出AD的长以及利用锐角三角函数关系求出∠DOA=60°进而利用扇形面积公式和三角形面积公式求出即可.
解答:
 解:连接BO,
解:连接BO,∵OC⊥AB,垂足为D,OC=12cm,CD=6cm,
∴AO=12cm,AD=
 =6
=6 cm,
cm,cos∠DOA=
 =
=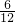 =
= ,
,∴AB=12
 cm,
cm,∴∠DOA=60°,
∴∠AOB=120°,
∴S扇形AOB-S△AOB=
 -
- ×6×12
×6×12 =(48π-36
=(48π-36 )cm2,
)cm2,故答案为:(48π-36
 )cm2.
)cm2.点评:此题主要考查了扇形的面积计算和垂径定理的应用,根据已知得出∠AOB的度数是解题关键.

练习册系列答案
相关题目
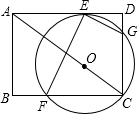 C于F,交CD于G.
C于F,交CD于G. (1997•西宁)如图,OC为半径,AB为弦,OC⊥AB,垂足为D,OC=12cm,CD=6cm.则S弓形ACB=
(1997•西宁)如图,OC为半径,AB为弦,OC⊥AB,垂足为D,OC=12cm,CD=6cm.则S弓形ACB=
 如图,OC为半径,AB为弦,OC⊥AB,垂足为D,OC=12cm,CD=6cm.则S弓形ACB= .
如图,OC为半径,AB为弦,OC⊥AB,垂足为D,OC=12cm,CD=6cm.则S弓形ACB= .