题目内容
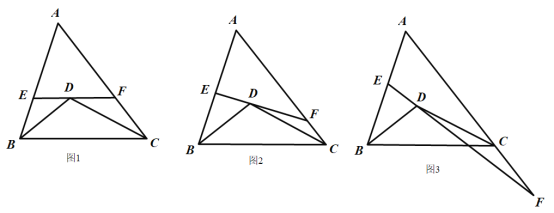
【题目】已知,在△ABC中,BD平分∠ABC,CD平分∠ACB,BD,CD交于点D,EF过点D交AB于点E,交AC于点F.
(1)如图1,若EF∥BC,则∠BDE+∠CDF的度数为 (用含有∠A的代数式表示);
(2)当直线EF绕点D旋转到如图2所示的位置时,(1)中的结论是否成立?请说明理由;
(3)当直线EF绕点D旋转到如图3所示的位置时,(1)中的结论是否成立?若成立,请说明理由;若不成立,请求出∠BDE,∠CDF与∠A之间的关系.
【答案】(1)![]() ;(2)成立,见解析;(3)不成立,∠BDE-∠CDF=
;(2)成立,见解析;(3)不成立,∠BDE-∠CDF=![]() ,理由见详解
,理由见详解
【解析】
(1)先根据平行线的性质得出![]() ,然后根据角平分线的定义和三角形的内角和定理得出
,然后根据角平分线的定义和三角形的内角和定理得出![]() ,整理即可得出答案;
,整理即可得出答案;
(2)先根据角平分线的定义和三角形内角和定理求出![]() ,然后再利用平角的定义即可得出
,然后再利用平角的定义即可得出![]() 即可得出答案;
即可得出答案;
(3)先根据角平分线的定义和三角形内角和定理求出![]() ,然后再利用
,然后再利用![]()
![]() 即可得出答案.
即可得出答案.
解:(1)![]() ,
,
![]() ,
,
∵BD平分∠ABC,CD平分∠ACB,
![]() .
.
![]() ,
,
![]()
即∠BDE+∠CDF=![]()
(2)成立,理由如下:
∵BD平分∠ABC,CD平分∠ACB,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即∠BDE+∠CDF=![]() .
.
(3)不成立,∠BDE-∠CDF=![]() ,理由如下:
,理由如下:
∵BD平分∠ABC,CD平分∠ACB,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]() ,
,
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目