Question

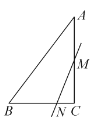
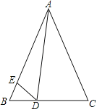
【题目】如图，在△ABC中，AB＝AC，点D、E分别在BC、AB上，且∠BDE＝∠CAD．

（1）求证：△BDE∽△CAD；

（2）求证：△ADE∽△ABD．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）由等腰三角形的性质得出∠B=∠C，结合已知条件∠BDE=∠CAD，即可证得结论；

（2）根据（1）的结论得到∠ADC=∠DEB，利用补角的性质可证得∠AED=∠ADB，再由公共角∠DAE=∠BAD，即可得出△ADE∽△ABD．

（1）∵AB=AC，
∴∠B=∠C，

∵∠BDE=∠CAD，
∴△BDE∽△CAD；

（2）∵△BDE∽△CAD，

∴∠ADC=∠DEB，

∴180-∠ADC=180-∠DEB，

∴∠AED=∠ADB，

又∵∠DAE=∠BAD，

∴△ADE∽△ABD．