��Ŀ����
����Ŀ�����˰��涨�ļ�������ij��ҩ���÷�ҩ��2Сʱ��ÿ����ѪҺ�еĺ�ҩ���ﵽ���ֵΪ4���ˣ���֪��ҩ��2Сʱǰÿ����ѪҺ�еĺ�ҩ��y�����ˣ���ʱ��x��Сʱ������������2Сʱ��y��x�ɷ���������ͼ��ʾ��������������Ϣ����������⣮ 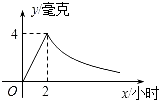
��1����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����ÿ����ѪҺ�еĺ�ҩ��������2����ʱ������Ч����ô���˷�ҩһ�����Ƽ�������Чʱ���Ƕ��
���𰸡�
��1���⣺�������������ı���ʽΪy=kx��
����ͼ��֪��������������ͼ���㣨2��4����
��2k=4�����k=2��
������������������ʽΪy=2x��0��x��2����
�跴���������ı���ʽΪy= ![]() ������ͼ��֪��������������ͼ���㣨2��4����
������ͼ��֪��������������ͼ���㣨2��4����
�� ![]() �����k=8��
�����k=8��
���ԣ�����ķ�������������Ϊy= ![]() ��x��2��
��x��2��
��2���⣺�����⣬��y=2ʱ����2x=2�����x=1��
![]() =2�����x=4��
=2�����x=4��
��4��1=3��Сʱ����
�𣺲��˷�ҩһ�Σ����Ƽ�������Чʱ����3Сʱ
����������1�����ݵ㣨2��4�����ô���ϵ��������������������ʽ�����ݵ㣨2��4�����ô���ϵ����������������ʽ����2����������������ʽ�������ֵ��2ʱ���Ա�����ֵ�����������Чʱ�䣮