题目内容
 (2013•丰台区二模)已知关于x的方程x2-(m-2)x+m-3=0.
(2013•丰台区二模)已知关于x的方程x2-(m-2)x+m-3=0.(1)求证:此方程总有两个实数根;
(2)设抛物线y=x2-(m-2)x+m-3与y轴交于点M,若抛物线与x轴的一个交点关于直线y=-x的对称点恰好是点M,求m的值.
分析:(1)通过该一元二次方程的根据的判别式△≥0可得此方程总有两个实数根;
(2)根据函数解析式易求得该函数图象与x、y轴的交点坐标,然后根据“抛物线与x轴的一个交点关于直线y=-x的对称点恰好是点M”可以列出-1=m-3或m-3=3-m,即m=2或m=3.
(2)根据函数解析式易求得该函数图象与x、y轴的交点坐标,然后根据“抛物线与x轴的一个交点关于直线y=-x的对称点恰好是点M”可以列出-1=m-3或m-3=3-m,即m=2或m=3.
解答:(1)证明:△=b2-4ac=(m-2)2-4(m-3)=m2-8m+16=(m-4)2≥0,
∴此方程总有两个实数根;
(2)解:抛物线y=x2-(m-2)x+m-3与y轴交点为M(0,m-3),
抛物线与x轴的交点为(1,0)和(m-3,0),它们关于直线y=-x的对称点分别为(0,-1)和(0,3-m).
由题意,可得:-1=m-3或m-3=3-m,即m=2或m=3.
∴此方程总有两个实数根;
(2)解:抛物线y=x2-(m-2)x+m-3与y轴交点为M(0,m-3),
抛物线与x轴的交点为(1,0)和(m-3,0),它们关于直线y=-x的对称点分别为(0,-1)和(0,3-m).
由题意,可得:-1=m-3或m-3=3-m,即m=2或m=3.
点评:本题考查了抛物线与x轴的交点、根的判别式.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系.
△=b2-4ac决定抛物线与x轴的交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;
△=b2-4ac=0时,抛物线与x轴有1个交点;
△=b2-4ac<0时,抛物线与x轴没有交点.
△=b2-4ac决定抛物线与x轴的交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;
△=b2-4ac=0时,抛物线与x轴有1个交点;
△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
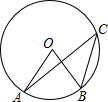 (2013•丰台区二模)如图,点A、B、C都在⊙O上,若∠AOB=68°,则∠ACB的度数为( )
(2013•丰台区二模)如图,点A、B、C都在⊙O上,若∠AOB=68°,则∠ACB的度数为( )