题目内容
(2004•温州)如图,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.求证:(1)∠EAF=∠B;(2)AF2=FE•FB.

【答案】分析:(1)欲证∠EAF=∠B,通过AB∥CD及已知发现它们都与∠C相等,等量转换即可;
(2)欲证AF2=FE•FB,可证△AFB∽△EFA得出.
解答:证明:(1)∵AB∥CD,
∴∠B=∠C,
又∵∠EAF=∠C,
∴∠EAF=∠B;
(2)在△AFB与△EFA中,
∵∠EAF=∠B,∠AFB=∠EFA,
∴△AFB∽△EFA,
∴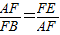 ,
,
即AF2=FE•FB.
点评:乘积的形式通常可以转化为比例的形式,由相似三角形的性质得出,同时考查了平行线的性质.
(2)欲证AF2=FE•FB,可证△AFB∽△EFA得出.
解答:证明:(1)∵AB∥CD,
∴∠B=∠C,
又∵∠EAF=∠C,
∴∠EAF=∠B;
(2)在△AFB与△EFA中,
∵∠EAF=∠B,∠AFB=∠EFA,
∴△AFB∽△EFA,
∴
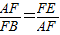 ,
,即AF2=FE•FB.
点评:乘积的形式通常可以转化为比例的形式,由相似三角形的性质得出,同时考查了平行线的性质.

练习册系列答案
相关题目
 VA.过点B作平行于底面的平面截得一个小圆锥,若小圆锥的侧面积为S1,原圆锥的侧面积为S,则下列判断中正确的是( )
VA.过点B作平行于底面的平面截得一个小圆锥,若小圆锥的侧面积为S1,原圆锥的侧面积为S,则下列判断中正确的是( )
 S
S S
S S
S S
S VA.过点B作平行于底面的平面截得一个小圆锥,若小圆锥的侧面积为S1,原圆锥的侧面积为S,则下列判断中正确的是( )
VA.过点B作平行于底面的平面截得一个小圆锥,若小圆锥的侧面积为S1,原圆锥的侧面积为S,则下列判断中正确的是( )
 S
S S
S S
S S
S
 VA.过点B作平行于底面的平面截得一个小圆锥,若小圆锥的侧面积为S1,原圆锥的侧面积为S,则下列判断中正确的是( )
VA.过点B作平行于底面的平面截得一个小圆锥,若小圆锥的侧面积为S1,原圆锥的侧面积为S,则下列判断中正确的是( )
 S
S S
S S
S S
S