题目内容
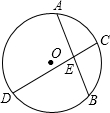如图，已知⊙O的弦AB、CD相交于点E，
的度数为60°，
的度数为100°，则∠AEC等于
- A.60°
- B.100°
- C.80°
- D.130°
C
分析：根据圆周角定理可求∠D=30°，∠A=50°，再根据三角形的外角与内角的关系，可求∠AEC．
解答：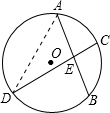
解：连接AD，
∵的度数为60°，
∴∠D=30°，
∵的度数为100°，
∴∠A=50°，
∴∠AEC=∠A+∠D=80°．
故选C．
点评：本题利用了三角形的外角与内角的关系和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
分析：根据圆周角定理可求∠D=30°，∠A=50°，再根据三角形的外角与内角的关系，可求∠AEC．
解答：
解：连接AD，∵
的度数为60°，∴∠D=30°，
∵
的度数为100°，∴∠A=50°，
∴∠AEC=∠A+∠D=80°．
故选C．
点评：本题利用了三角形的外角与内角的关系和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
如图，已知⊙O的弦CD垂直于直径AB，点E在CD上，且EC=EB．
23、如图，已知⊙O的弦AB垂直于直径CD，垂足为F，连接CA、CB．
如图，已知⊙O的弦AB、CD相交于点E， |
| AC |
|
| BD |
| A、60° | B、100° |
| C、80° | D、130° |
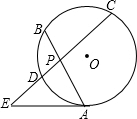如图，已知⊙O的弦AB、CD相交于点P，PA=4cm，PB=3cm，PC=6cm，EA切⊙O于点A，AE与CD的延长线交于点E，若AE=2| 5 |
| A、4cm | ||
| B、3cm | ||
| C、5cm | ||
D、
|
如图，已知⊙O的弦AC=2cm，∠ABC=45°，则图中阴影部分的面积是