题目内容
 作图、证明与计算
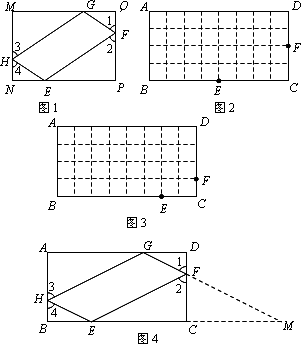
作图、证明与计算如图,在单位长度为1的正方形网格中,△ABC的三个顶点均在格点上,E为BC中点,请按要求完成下列各题:
(1)画AD∥BC(D为格点),连接CD;
(2)判断四边形ABCD的形状;
(3)求sin∠ADC的值和tan∠CAE的值;
(4)求△ABC的外接圆半径和内切圆半径(保留根号)
分析:(1)根据题目要求结合网格画图即可;
(2)根据勾股定理求得BC=AD.则由“有一组对边平行且相等是四边形是平行四边形”得到四边形ABCD是平行四边形;
(3)在网格中利用直角三角形,先求BC2,AB2,AC2的值,再比较列出等式,判断直角三角形;把问题转化到Rt△ACF,Rt△ADC中,利用三角函数的定义解题;
(4)直角三角形的内切圆半径和其三边有特殊关系:三边中a b为直角边,c为斜边,内切圆半径为r,则r=
;外接圆的半径就是斜边的一半.
(2)根据勾股定理求得BC=AD.则由“有一组对边平行且相等是四边形是平行四边形”得到四边形ABCD是平行四边形;
(3)在网格中利用直角三角形,先求BC2,AB2,AC2的值,再比较列出等式,判断直角三角形;把问题转化到Rt△ACF,Rt△ADC中,利用三角函数的定义解题;
(4)直角三角形的内切圆半径和其三边有特殊关系:三边中a b为直角边,c为斜边,内切圆半径为r,则r=
| 1 |
| 2 |
解答: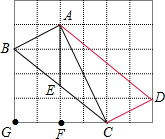 解:(1)如图所示;
解:(1)如图所示;
(2)四边形ABCD是平行四边形.理由如下:
根据勾股定理得到BC=AD=
=5.
又∵AD∥BC,
∴四边形ABCD是平行四边形;
(3)由图象可知AB2=12+22=5,AC2=22+42=20,BC2=32+42=25,
∴BC2=AB2+AC2,
∴∠CAB=90°,即△ABC是直角三角形.
∵BG∥AF,F为CG的中点,
∴BC的中点E在线段AF上,
由图象可知CD=
,AD=5,
∴sin∠CAD=
=
,tan∠CAE=tan∠CAF=
=
;
(4)由(1)知,BC=5,且由(3)知,△ABC是直角三角形,BC是斜边,则△ABC的外接圆半径=
=
;
如图,根据勾股定理得到AB=
,AC=2
,BC=5,则△ABC的内切圆半径=
×(AB+AC-BC)=
.
 解:(1)如图所示;
解:(1)如图所示;(2)四边形ABCD是平行四边形.理由如下:
根据勾股定理得到BC=AD=
| 42+32 |
又∵AD∥BC,
∴四边形ABCD是平行四边形;
(3)由图象可知AB2=12+22=5,AC2=22+42=20,BC2=32+42=25,
∴BC2=AB2+AC2,
∴∠CAB=90°,即△ABC是直角三角形.
∵BG∥AF,F为CG的中点,
∴BC的中点E在线段AF上,
由图象可知CD=
| 5 |
∴sin∠CAD=
| CD |
| AD |
| ||
| 5 |
| 2 |
| 4 |
| 1 |
| 2 |
(4)由(1)知,BC=5,且由(3)知,△ABC是直角三角形,BC是斜边,则△ABC的外接圆半径=
| BC |
| 2 |
| 5 |
| 2 |
如图,根据勾股定理得到AB=
| 5 |
| 5 |
| 1 |
| 2 |
3
| ||
| 2 |
点评:本题考查了圆的综合题.解题时,充分利用了勾股定理及其逆定理的运用,锐角三角函数的定义,关键是运用网格表示线段的长度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
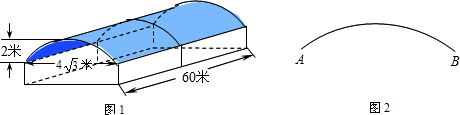
 如图AB、CD是两条垂直的公路,设计时想在拐弯处用一段圆弧形弯道把它们连接起来(圆弧在B、D两处分别与道路相切),测得BC=100米,∠PBC=45°.
如图AB、CD是两条垂直的公路,设计时想在拐弯处用一段圆弧形弯道把它们连接起来(圆弧在B、D两处分别与道路相切),测得BC=100米,∠PBC=45°.