题目内容
【题目】若直线y=2x+t﹣3与函数y=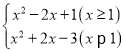
的图象有且只有两个公共点时，则t的取值范围是 ．
【答案】t=0或t＞1.
【解析】
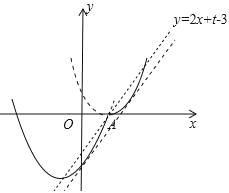
试题分析：画出函数图象，利用图象分两种情形讨论即可．当直线y=2x+t﹣3经过点A（1，0）时，直线与函数y的图象有3个交点，此时0=2+t﹣3，解得t=1，观察图象可知，t＞1时，直线y=2x+t﹣3与函数y的图象有且只有两个公共点，当直线y=2x+t﹣3与y=
﹣2x+1相切时，则有﹣4x﹣t+4=0，∵△=0，∴16﹣4t﹣16=0，∴t=0，此时直线为y=2x﹣3，由
，解得
，∴直线与y=+2x﹣3只有一个交点，∴t=0时，直线y=2x﹣3与函数y有两个交点，综上所述，t＞1或t=0时，直线y=2x+t﹣3与函数y的图象有且只有两个公共点．
故答案为：t=0或t＞1．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
相关题目
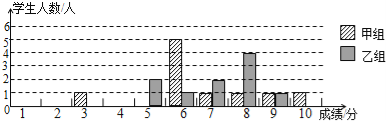
【题目】某校团委举办了一次“中国梦，我的梦”演讲比赛，满分10分，学生得分均为整数，成绩达6分以上为合格，达到9分以上（含9分）为优秀．这次竞赛中甲、乙两组学生成绩分布的条形统计图如下．
（1）补充完成下列的成绩统计分析表：
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲 | 6.7 | | 3.41 | 90% | 20% |
乙 | | 7.5 | | 80% | 10% |
（2）小明同学说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上！”观察上表可知，小明是 组学生；（填“甲”或“乙”）
（3）甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组．但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组．请你给出两条支持乙组同学观点的理由．
