题目内容
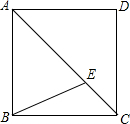正方形ABCD的对角线AC上有一点E，AE=AB，则∠ABE=________．
67.5°
分析：根据正方形性质求出∠BAC=45°，根据等腰三角形性质求出∠ABE=∠AEB，在△ABE中，根据三角形的内角和定理求出即可
解答：∵四边形ABCD是正方形，
∴∠BAD=90°，∠BAC=
∠BAD=45°，
∵AE=AB，
∴∠ABE=∠AEB，
∵∠ABE+∠AEB+∠BAC=180°，
∴∠ABE=（180°-45°）=67.5°，
故答案为：67.5°．
点评：本题考查了等腰三角形的性质，三角形的内角和定理，正方形的性质的应用，主要考查学生运用性质进行推理的能力，题目比较好，但难度不大．
分析：根据正方形性质求出∠BAC=45°，根据等腰三角形性质求出∠ABE=∠AEB，在△ABE中，根据三角形的内角和定理求出即可
解答：∵四边形ABCD是正方形，
∴∠BAD=90°，∠BAC=
∠BAD=45°，∵AE=AB，
∴∠ABE=∠AEB，
∵∠ABE+∠AEB+∠BAC=180°，
∴∠ABE=
（180°-45°）=67.5°，故答案为：67.5°．
点评：本题考查了等腰三角形的性质，三角形的内角和定理，正方形的性质的应用，主要考查学生运用性质进行推理的能力，题目比较好，但难度不大．
练习册系列答案
挑战100单元检测试卷系列答案
名题金卷系列答案
相关题目
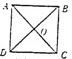8、如图，正方形ABCD的对角AC，BD交于点O，，则结论①AB=BC=CD=DA；②AO=BO=CO=DO；③AC⊥BD中正确的有（ ）
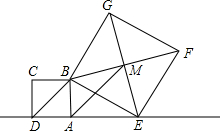如图，已知正方形ABCD的边长为1，点E是射线DA一动点（DE＞1），连结BE，以BE为边在BE上方作正方形BEFG，设M为正方形BEFG的中心，如果定义：只有一组对角是直角的四边形叫做损矩形．
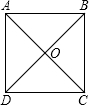如图，正方形ABCD的对角AC，BD交于点O，则结论①AB=BC=CD=DA；②AO=BO=CO=DO；③AC⊥BD中正确的有
