题目内容
【题目】如图,DE∥BC,∠D:∠DBC=2:1,∠1=∠2,求∠DEB的度数. 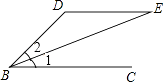
【答案】解:设∠1为x, ∵∠1=∠2,
∴∠2=x,
∴∠DBC=∠1+∠2=2x,
∵∠D:∠DBC=2:1,
∴∠D=2×2x=4x,
∵DE∥BC,
∴∠D+∠DBC=180°,
即2x+4x=180°,
解得x=30°,
∵DE∥BC,
∴∠DEB=∠1=30°.
【解析】设∠1为x,所以∠DBC为2x,∠D为4x,根据两直线平行,同旁内角互补列出方程即可求出∠1的度数,再根据两直线平行,内错角相等即可求出∠DEB.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
【题目】某校随机抽查了10名参加2016年云南省初中学业水平考试学生的体育成绩,得到的结果如表:
成绩(分) | 46 | 47 | 48 | 49 | 50 |
人数(人) | 1 | 2 | 1 | 2 | 4 |
下列说法正确的是( )
A.这10名同学的体育成绩的众数为50
B.这10名同学的体育成绩的中位数为48
C.这10名同学的体育成绩的方差为50
D.这10名同学的体育成绩的平均数为48