题目内容
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,
若∠1=35°,则∠2的度数为
| A.10° | B.20° | C.25° | D.30° |
C
解析分析:如图,延长AB交CF于E,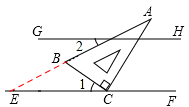
∵∠ACB=90°,∠A=30°,∴∠ABC=60°。
∵∠1=35°,∴∠AEC=∠ABC﹣∠1=25°。
∵GH∥EF,∴∠2=∠AEC=25°。
故选C。

练习册系列答案
相关题目
已知∠α=70°,则∠α的补角为( )
| A.120° | B.110° | C.70° | D.20° |
以下四个命题:①在同一平面内,过一点有且只有一条直线与已知直线垂直;②若a>b,则-2a>-2b;③如果三条直线a、b、c满足:a∥b,b∥c,那么直线a与直线c必定平行;④对顶角相等,其中真命题有( )个.
| A.1 | B.2 | C.3 | D.4 |
下列四个条件中能判断两条直线互相垂直的有( )
①两条直线相交所成的四个角中有一个角是直角;
②两条直线相交所成的四个角相等;
③两条直线相交所成的四个角中有一组相邻的角相等;
④两条直线相交所成的四个角中有一组对顶角的和为180°.
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,AB∥CD,CE平分∠BCD,∠DCE=18°,则∠B等于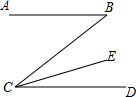
| A.18° | B.36° | C.45° | D.54° |

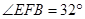 ,则①
,则① 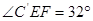 ②
② 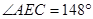 ③
③ 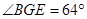
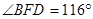 以上结论正确的有 .(填序号)
以上结论正确的有 .(填序号)