Question

【题目】如图，O为直线AB上一点，OD平分∠AOC，OE平分∠COB，

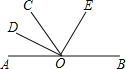
①问：DO与OE有何关系？并说明你的理由．

②图中有几对互余的角？试写出所有你认为互余的角．

Answer 1

【答案】①OD⊥OE，理由见解析；②互余的角有：∠AOD与∠COE，∠AOD与∠BOE，∠DOC与∠COE，∠DOC与∠BOE．

【解析】

试题分析：①直接利用角平分线的性质结合平角的定义得出∠DOE=（∠AOC+∠BOC）=90°，进而求出答案；

②利用①中所求，得出互余的两角即可．

解：①OD⊥OE，

理由：∵O为直线AB上一点，OD平分∠AOC，OE平分∠COB，

∴∠AOD=∠DOC，∠BOE=∠COE，

∴∠DOE=（∠AOC+∠BOC）=90°，

∴OD⊥OE；

②由①可得互余的角有：∠AOD与∠COE，∠AOD与∠BOE，∠DOC与∠COE，∠DOC与∠BOE．