题目内容
【题目】在平面坐标坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的变换点
的变换点![]() 的坐标定义如下:当
的坐标定义如下:当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ;当
;当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .
.
已知点![]() ,点
,点![]() ,点
,点![]() .
.
(![]() )点
)点![]() 的变换点
的变换点![]() 的坐标是__________.
的坐标是__________.
点![]() 的变换点为
的变换点为![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() __________.
__________.
(![]() )点
)点![]() 的变换点为
的变换点为![]() ,随着
,随着![]() 的变化,点
的变化,点![]() 会运动起来,请在备用图(
会运动起来,请在备用图(![]() )中画出点
)中画出点![]() 的运动路径.
的运动路径.
(![]() )若
)若![]() 是等腰三角形,请直接写出此时
是等腰三角形,请直接写出此时![]() 的值:__________.
的值:__________.
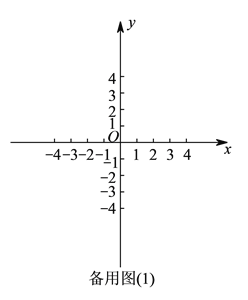

【答案】(![]() )
)![]() ;
;![]() .(
.(![]() )点
)点![]() 的运动路径见解析.(
的运动路径见解析.(![]() )见解析.
)见解析.
【解析】试题分析:
(1)①按照变换点的定义写出A′的坐标即可;②按照变换点的定义根据点B的坐标写出点B′的坐标,如图,过点B作BD⊥x轴于点D,过点B′作B′E⊥x轴于点E,则由已知易证△BDO≌△OEB′,从而可证得∠BOD=∠OB′E,结合∠OB′E+∠EOB′=90°,即可证得∠BOB′=90°;
(2)①由变换点的定义可得,当n<2时,点C(2,n)的变换点的坐标是(-2,n);②当![]() 时,点C(2,n)的变换点的坐标是(-n,2),由此即可画出点C的运动路线;
时,点C(2,n)的变换点的坐标是(-n,2),由此即可画出点C的运动路线;
(3)由题意可知:![]() ,
,![]() ,连接
,连接![]() ,以
,以![]() 为圆心,
为圆心,![]() 长度为半径作圆,交点
长度为半径作圆,交点![]() 的运动路径于点
的运动路径于点![]() ;以
;以![]() 为圆心,
为圆心,![]() 长为半径作圆,交点
长为半径作圆,交点![]() 的运动路径于点
的运动路径于点![]() ,
,![]() ;作线段
;作线段![]() 的垂直平分线,交点
的垂直平分线,交点![]() 的运动路径于点
的运动路径于点![]() ,
,![]() ;如图所示,
;如图所示,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均为所求点
均为所求点![]() 的位置,再根据已知条件计算出对应的n的值即可.
的位置,再根据已知条件计算出对应的n的值即可.
试题解析:
(![]() )∵
)∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
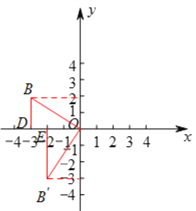
(![]() )点
)点![]() 的运动路径如图所示:
的运动路径如图所示:
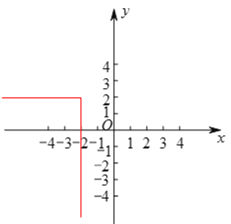
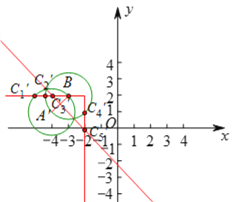
(![]() )如图:
)如图:![]() ,
,![]() ,连接
,连接![]() ,
,
以![]() 为圆心,
为圆心,![]() 长度为半径作圆,交点
长度为半径作圆,交点![]() 的运动路径于点
的运动路径于点![]() ,
,
以![]() 为圆心,
为圆心,![]() 长为半径作圆,交点
长为半径作圆,交点![]() 的运动路径于点
的运动路径于点![]() ,
,![]() ,
,
作线段![]() 的垂直平分线,交点
的垂直平分线,交点![]() 的运动路径于点
的运动路径于点![]() ,
,![]() ,
,
如图所示,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均为所求点
均为所求点![]() 的位置,
的位置,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
综上所述,![]() 的值是
的值是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

 阅读快车系列答案
阅读快车系列答案