Question

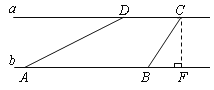
【题目】河流两岸a、b互相平行，C、D是河岸a上间隔50m的两个电线杆．某人在河岸b上的A处测得∠DAB=30°，然后沿河岸走了100m到达B处，测得∠CBF=60°，求河流的宽度CF的值（结果精确到个位）．

Answer 1

【答案】43

【解析】试题分析：本题可将已知的条件构建到直角三角形中进行计算，过点C作CE∥AD，交AB于E，那么∠CEF=∠DAB=30°且AE=CD=50，根据观察发现，

∠CBF=∠CEB+∠ECB=60°，而∠CEB=30°，那么∠ECB=∠CEB，那么CB=BE，直角三角形CBF中，有了CB的长，有锐角的度数，CF的值便可求出来了．

试题解析：

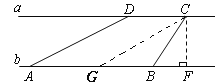
作CG∥AD，∠CGB=∠BCG= 300

则BC=BG=50，BF=25，CF=≈43米