题目内容
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处。
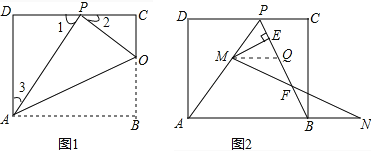
(I)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.若△OCP与△PDA的面积比为1︰4,求边CD的长.
(Ⅱ)如图2,在(Ⅰ)的条件下,擦去折痕AO、线段OP,连接BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问当动点M、N在移动的过程中,线段EF的长度是否发生变化?若变化,说明变化规律.若不变,求出线段EF的长度.

【答案】(1)10;(2)![]() .
.
【解析】试题分析:(1)先证出∠C=∠D=90°,再根据∠1+∠3=90°,∠1+∠2=90°,得出∠2=∠3,即可证出△OCP∽△PDA;根据△OCP与△PDA的面积比为1:4,得出CP=![]() AD=4,设OP=x,则CO=8﹣x,由勾股定理得列方程,求出x,最后根据CD=AB=2OP即可求出边CD的长;
AD=4,设OP=x,则CO=8﹣x,由勾股定理得列方程,求出x,最后根据CD=AB=2OP即可求出边CD的长;
(2)作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据ME⊥PQ,得出EQ=![]() PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=
PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=![]() QB,再求出EF=
QB,再求出EF=![]() PB,由(1)中的结论求出PB的长,最后代入EF=
PB,由(1)中的结论求出PB的长,最后代入EF=![]() PB即可得出线段EF的长度不变.
PB即可得出线段EF的长度不变.
试题解析:(1)如图1,∵四边形ABCD是矩形,∴∠C=∠D=90°,∴∠1+∠3=90°,∵由折叠可得∠APO=∠B=90°,∴∠1+∠2=90°,∴∠2=∠3,又∵∠D=∠C,∴△OCP∽△PDA;∵△OCP与△PDA的面积比为1:4,∴![]() =
=![]() ,∴CP=
,∴CP=![]() AD=4,设OP=x,则CO=8﹣x,在Rt△PCO中,∠C=90°,由勾股定理得 :
AD=4,设OP=x,则CO=8﹣x,在Rt△PCO中,∠C=90°,由勾股定理得 :![]() ,解得:x=5,∴CD=AB=AP=2OP=10,∴边CD的长为10;
,解得:x=5,∴CD=AB=AP=2OP=10,∴边CD的长为10;
(2)作MQ∥AN,交PB于点Q,如图2,∵AP=AB,MQ∥AN,∴∠APB=∠ABP=∠MQP,∴MP=MQ,∵BN=PM,∴BN=QM.∵MP=MQ,ME⊥PQ,∴EQ=![]() PQ.∵MQ∥AN,∴∠QMF=∠BNF,在△MFQ和△NFB中,∵∠QFM=∠NFB,∠QMF=∠BNF,MQ=BN,∴△MFQ≌△NFB(AAS),∴QF=
PQ.∵MQ∥AN,∴∠QMF=∠BNF,在△MFQ和△NFB中,∵∠QFM=∠NFB,∠QMF=∠BNF,MQ=BN,∴△MFQ≌△NFB(AAS),∴QF=![]() QB,∴EF=EQ+QF=
QB,∴EF=EQ+QF=![]() PQ+
PQ+![]() QB=
QB=![]() PB,由(1)中的结论可得:PC=4,BC=8,∠C=90°,∴PB=
PB,由(1)中的结论可得:PC=4,BC=8,∠C=90°,∴PB=![]() =
=![]() ,∴EF=
,∴EF=![]() PB=
PB=![]() ,∴在(1)的条件下,当点M、N在移动过程中,线段EF的长度不变,它的长度为
,∴在(1)的条件下,当点M、N在移动过程中,线段EF的长度不变,它的长度为![]() .
.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案