题目内容
【题目】如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
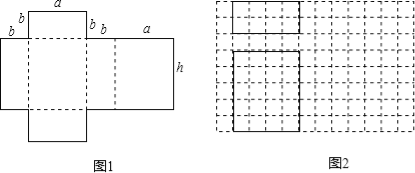
(1)这个几何体模型的名称是 .
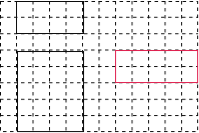
(2)如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
(3)若h=a+b,且a,b满足![]() a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
【答案】(1)长方体或底面为长方形的直棱柱;(2)图形略;(3)62.
【解析】试题分析:(1)观察平面展开图,侧面四个面是长方形,且上下两个底面也是长方形,所以折叠后能围成长方体.(2)根据图1所标注的相关线段的长度画出长方体,根据立体图形和相关线段的长度画出其左视图;(3)将给出的式子中10拆分成1+9,则所给式子写成两个完全平方式,因式分解后能求出a、b的值,则h的值就能求出,然后由长方体的表面积计算公式求解.
试题解析:(1)由平面展开图得知,侧面四个面是长方形,且上下两个底面也是长方形,∴折叠后能围成长方体.(2)根据图1所标注的相关线段的长度和给出的视图画出长方体,是长宽高分别为4,5,2的长方体,则左视图是长为5,宽为2的长方形;画出图形,如图:
(3)将给出的式子中10拆分成1+9,则所给式子写成两个完全平方式,(![]() a﹣1)2+(b﹣3)2=0,则
a﹣1)2+(b﹣3)2=0,则![]() a﹣1=0,b﹣3=0,∴a=2,b=3,所以h=a+b=2+3=5.所以此长方体的表面积为六个面的面积和:2(2×3+5×2+3×5)=62.
a﹣1=0,b﹣3=0,∴a=2,b=3,所以h=a+b=2+3=5.所以此长方体的表面积为六个面的面积和:2(2×3+5×2+3×5)=62.

练习册系列答案
相关题目