��Ŀ����
����Ŀ����֪����AOB��
��������A'O'B'��ʹ��A'O��B'=��AOB
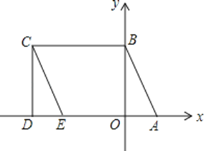
��1����ͼ1���Ե�OΪԲ�ģ����ⳤΪ�뾶�������ֱ�OA��OB�ڵ�C��D��
��2����ͼ2����һ������O��A�䣬�Ե�O��ΪԲ�ģ�OC��Ϊ�뾶�仡����O��A���ڵ�C�䣻
��3���Ե�C��ΪԲ�ģ�CD��Ϊ�뾶���������2���������Ļ����ڵ�D�䣻
��4������D�仭����O��B'������A'O'B'=��AOB��
����������ͼ���裬����֤����A'O'B��=��AOB��
���𰸡�֤��������.
��������
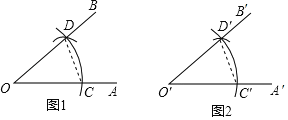
�ɻ�����ͼ�õ�OD=OC=O��D��=O��C�䣬CD=C��D�����������SSS����֤����OCD�ա�O��C��D����Ȼ������ȫ�������ε����ʿɵõ���A'O'B��=��AOB��
��������OD=OC=O��D��=O��C�䣬CD=C��D�䣬
����OCD����O��C��D����
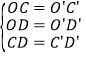 ��
��
���OCD�ա�O��C��D�䣬
���COD=��C��O��D�䣬
����A'O'B��=��AOB��

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ