题目内容
33、探索规律:
观察下面由“※”组成的图案和算式,解答问题:

(1)请猜想1+3+5+7+9+…+19=
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n+1)+(2n+3)=
(3)请用上述规律计算:103+105+107+…+2007+2009=
观察下面由“※”组成的图案和算式,解答问题:

(1)请猜想1+3+5+7+9+…+19=
102
;(2)请猜想1+3+5+7+9+…+(2n-1)+(2n+1)+(2n+3)=
(n+2)2
;(3)请用上述规律计算:103+105+107+…+2007+2009=
1007424
.分析:对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目的难点.
解答:解:(1)由图片知:
第1个图案所代表的算式为:1=12;
第2个图案所代表的算式为:1+3=4=22;
第3个图案所代表的算式为:1+3+5=9=32;
…
依次类推:第n个图案所代表的算式为:1+3+5+…+(2n-1)=n2;
故当2n-1=19,即n=10时,1+3+5+…+19=102.
(2)由(1)可知:1+3+5+7+9+…+(2n-1)+(2n+1)+(2n+3)=(n+2)2.
(3)103+105+107++2007+2009
=(1+3++2007+2009)-(1+3++99+101)
=10052-512
=1007424.
第1个图案所代表的算式为:1=12;
第2个图案所代表的算式为:1+3=4=22;
第3个图案所代表的算式为:1+3+5=9=32;
…
依次类推:第n个图案所代表的算式为:1+3+5+…+(2n-1)=n2;
故当2n-1=19,即n=10时,1+3+5+…+19=102.
(2)由(1)可知:1+3+5+7+9+…+(2n-1)+(2n+1)+(2n+3)=(n+2)2.
(3)103+105+107++2007+2009
=(1+3++2007+2009)-(1+3++99+101)
=10052-512
=1007424.
点评:主要考查了学生通过特例分析从而归纳总结出一般结论的能力.

练习册系列答案
相关题目
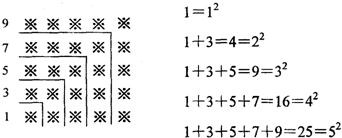

 32、探索规律:观察下面由※组成的图案和算式,解答问题:
32、探索规律:观察下面由※组成的图案和算式,解答问题: 探索规律:观察下面由※组成的图案和算式,解答问题:
探索规律:观察下面由※组成的图案和算式,解答问题: 探索规律:观察下面由※组成的图案和算式,
探索规律:观察下面由※组成的图案和算式,