题目内容
解答题①当m取何值时,关于x的方程:3x-2=4与5x-1=-m的解相等?
②一堆小麦用8个编织袋来装,以每袋55千克为标准,超过的记作为正数,不足的记作为负数,现记录如下:(单位:千克)
+2,-3,+2,+1,-2,-1,0,-2
(1)这堆小麦共重多少千克?
(2)若每千克小麦的售价为1.2元,则这堆小麦可卖多少钱?
③探索规律:观察下面由“※”组成的图案和算式,解答问题:
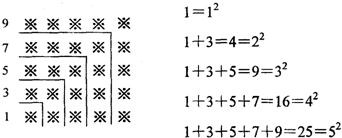
(1)请猜想1+3+5+7+9+…+19=
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n+1)=
(3)请用上述规律计算:103+105+107+…+2003+2005.
④在左边的日历中,用一个正方形任意圈出二行二列四个数,
如

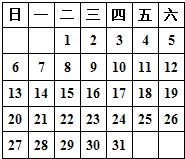
若在第二行第二列的那个数表示为a,其余各数分别为b,c,d.
如
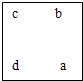
(1)分别用含a的代数式表示b,c,d这三个数.
(2)求这四个数的和(用含a的代数式表示,要求合并同类项化简)
(3)这四个数的和会等于51吗?如果会,请算出此时a的值,如果不会,说明理由.(要求列方程解答)
分析:①先解方程3x-2=4,再把x的值代入5x-1=-m,即可求出m的值;
②(1)先求出称重记录即八个数的和,再加上55乘以8的积,即可求得这堆小麦的重量;(2)用单价1.2乘以这堆小麦的重量,即可求得这堆小麦所卖价钱;
③由1=12;1+3=22;1+3+5=32;1+3+5+7=16=42;1+3+5+7+9=25=52,由此可以得出从1开始连续的奇数的和等于相加的项数的平方,据此求解(1)(2);(3)103+105+107+…+2005可看作(1+3+…+2005)-(1+3+…+99+101);
④观察4个数之间的大小关系,可以看出同一行相邻的数是连续的自然数,同一列相邻的两个数相隔7.(1)如果第二行第二列的那个数表示为a,据此可分别表示b,c,d;(2)即求a+b+c+d的值,把(1)的结果代入,再合并同类项即可;(3)由题意知a、b、c、d四个数的和为51,把(2)的结果代入,若算出的a是正整数,则符合题意,否则就不合题意.
②(1)先求出称重记录即八个数的和,再加上55乘以8的积,即可求得这堆小麦的重量;(2)用单价1.2乘以这堆小麦的重量,即可求得这堆小麦所卖价钱;
③由1=12;1+3=22;1+3+5=32;1+3+5+7=16=42;1+3+5+7+9=25=52,由此可以得出从1开始连续的奇数的和等于相加的项数的平方,据此求解(1)(2);(3)103+105+107+…+2005可看作(1+3+…+2005)-(1+3+…+99+101);
④观察4个数之间的大小关系,可以看出同一行相邻的数是连续的自然数,同一列相邻的两个数相隔7.(1)如果第二行第二列的那个数表示为a,据此可分别表示b,c,d;(2)即求a+b+c+d的值,把(1)的结果代入,再合并同类项即可;(3)由题意知a、b、c、d四个数的和为51,把(2)的结果代入,若算出的a是正整数,则符合题意,否则就不合题意.
解答:解:①解方程3x-2=4,得x=2,
把x=2代入5x-1=-m,得m=-9.
故当m=-9时,关于x的方程:3x-2=4与5x-1=-m的解相等;
②(1)+2-3+2+1-2-1+0-2=-3,-3+55×8=437.
故这堆小麦共重437千克;
(2)1.2×437=524.4.
故若每千克小麦的售价为1.2元,则这堆小麦可卖524.4元;
③由图案1,3,5,7,9是连续的几个奇数;
由算式:1=12,
1+3=22,从1开始连续2项奇数和;
1+3+5=32,从1开始连续3项奇数和;
1+3+5+7=16=42,从1开始连续4项奇数和;
1+3+5+7+9=25=52,从1开始连续5项奇数和;
可以得出规律:从1开始连续n个奇数的和等于n2,
所以:(1)1+3+5+7+9+…+19=102,从1开始连续10个奇数相加;
(2)1+3+5+7+9+…+(2n+1)=(n+1)2,从1开始n+1个奇数相加.
(3)103+105+107+…+2005=(1+3+…+2005)-(1+3+…+99+101)=10032-512=1003408;
故答案为102,(n+1)2,10032-512=1003408;
④(1)在第二行第二列的数为a,则其余3个数分别是b=a-7,c=a-8,d=a-1;
(2)a+b+c+d=a+a-7+a-8+a-1=4a-16;
(3)假设这四个数的和等于51,由(2)知4a-16=51,
解得a=16
.
∵16
不是正整数,不合题意.
故这四个数的和不会等于51.
把x=2代入5x-1=-m,得m=-9.
故当m=-9时,关于x的方程:3x-2=4与5x-1=-m的解相等;
②(1)+2-3+2+1-2-1+0-2=-3,-3+55×8=437.
故这堆小麦共重437千克;
(2)1.2×437=524.4.
故若每千克小麦的售价为1.2元,则这堆小麦可卖524.4元;
③由图案1,3,5,7,9是连续的几个奇数;
由算式:1=12,
1+3=22,从1开始连续2项奇数和;
1+3+5=32,从1开始连续3项奇数和;
1+3+5+7=16=42,从1开始连续4项奇数和;
1+3+5+7+9=25=52,从1开始连续5项奇数和;
可以得出规律:从1开始连续n个奇数的和等于n2,
所以:(1)1+3+5+7+9+…+19=102,从1开始连续10个奇数相加;
(2)1+3+5+7+9+…+(2n+1)=(n+1)2,从1开始n+1个奇数相加.
(3)103+105+107+…+2005=(1+3+…+2005)-(1+3+…+99+101)=10032-512=1003408;
故答案为102,(n+1)2,10032-512=1003408;
④(1)在第二行第二列的数为a,则其余3个数分别是b=a-7,c=a-8,d=a-1;
(2)a+b+c+d=a+a-7+a-8+a-1=4a-16;
(3)假设这四个数的和等于51,由(2)知4a-16=51,
解得a=16
| 3 |
| 4 |
∵16
| 3 |
| 4 |
故这四个数的和不会等于51.
点评:本题考查了一元一次方程的解法及应用,有理数的运算,通过特例分析从而归纳总结出一般结论的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



