题目内容
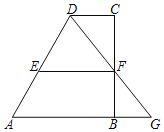
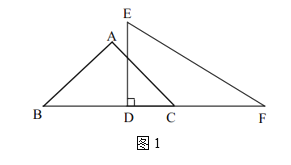
【题目】将两块直角三角板如图1放置,等腰直角三角板![]() 的直角顶点是点
的直角顶点是点![]() ,
,![]() ,直角板
,直角板![]() 的直角顶点
的直角顶点![]() 在
在![]() 上,且
上,且![]() ,
,![]() .三角板
.三角板![]() 固定不动,将三角板
固定不动,将三角板![]() 绕点
绕点![]() 逆时针旋转,旋转角为
逆时针旋转,旋转角为![]()
![]() .
.
(1)当![]() _______时,
_______时,![]() ;
;
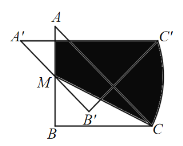
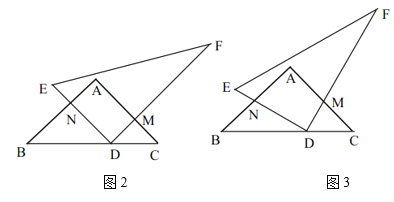
(2)当![]() 时,三角板
时,三角板![]() 绕点
绕点![]() 逆时针旋转至如图2位置,设
逆时针旋转至如图2位置,设![]() 与
与![]() 交于点
交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.
(3)如图3,设![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的表达式(不用写
的表达式(不用写![]() 的取值范围).
的取值范围).
【答案】(1)30°;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据两直线平行,内错角相等可得∠MDC=∠F,再根据旋转的性质可得旋转角α=∠MDC;
(2)根据旋转的性质可得∠MDC=α=45°,再根据等腰三角形的性质可得∠C=45°,然后求出∠DMC=90°,同理可求∠DNA=90°,然后求出四边形ANDM是矩形,再根据△DNA和△BAC相似,利用相似三角形对应边成比例列式求出DM=1,同理求出DN=2,最后根据矩形的面积公式列式计算即可得解;
(3)过![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,根据同角的余角相等求出
,根据同角的余角相等求出![]() ,然后求出
,然后求出![]() 相似,利用相似三角形对应边成比例列式求出
相似,利用相似三角形对应边成比例列式求出![]() ,然后表示MH1,再表示出BN,最后根据四边形ANDM的面积
,然后表示MH1,再表示出BN,最后根据四边形ANDM的面积![]() ,列式整理即可得解.
,列式整理即可得解.
解:(1)∵![]() ,
,
∴∠MDC=∠F,
∴旋转角![]() 度;
度;
(2)当![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
同理![]() ,
,
又![]() ,
,
![]() 四边形
四边形![]() 为矩形
为矩形
![]() ,
,
![]() ,
,
∴![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 同理得
同理得![]()
![]() ;
;
(3)如图3,过![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]()
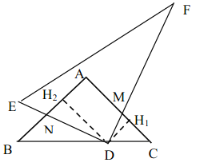
图3
由(2)知四边形为![]() 矩形,
矩形,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
相关题目