题目内容
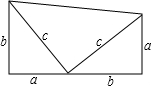 如图所示,这是美国第20任总统加菲尔德证明勾股定理时所采用的图形,是用两个全等的直角三角形和一个等腰直角三角形拼出一个梯形.借助这个图形,你能用面积法来验证勾股定理吗?
如图所示,这是美国第20任总统加菲尔德证明勾股定理时所采用的图形,是用两个全等的直角三角形和一个等腰直角三角形拼出一个梯形.借助这个图形,你能用面积法来验证勾股定理吗?
解:此图可以这样理解,有三个Rt△其面积分别为 ab,
ab, ab和
ab和 c2.
c2.
还有一个直角梯形,其面积为 (a+b)(a+b).
(a+b)(a+b).
由图形可知: (a+b)(a+b)=
(a+b)(a+b)= ab+
ab+ ab+
ab+ c2
c2
整理得(a+b)2=2ab+c2,a2+b2+2ab=2ab+c2,
∴a2+b2=c2.
由此验证勾股定理.
分析:用三角形的面积和、梯形的面积来表示这个图形的面积,从而证明勾股定理.
点评:此题主要利用了三角形的面积公式:底×高÷2,和梯形的面积公式:(上底+下底)×高÷2.
 ab,
ab, ab和
ab和 c2.
c2.还有一个直角梯形,其面积为
 (a+b)(a+b).
(a+b)(a+b).由图形可知:
 (a+b)(a+b)=
(a+b)(a+b)= ab+
ab+ ab+
ab+ c2
c2整理得(a+b)2=2ab+c2,a2+b2+2ab=2ab+c2,
∴a2+b2=c2.
由此验证勾股定理.
分析:用三角形的面积和、梯形的面积来表示这个图形的面积,从而证明勾股定理.
点评:此题主要利用了三角形的面积公式:底×高÷2,和梯形的面积公式:(上底+下底)×高÷2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
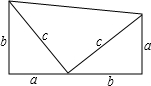 如图所示,这是美国第20任总统加菲尔德证明勾股定理时所采用的图形,是用两个全等的直角三角形和一个等腰直角三角形拼出一个梯形.借助这个图形,你能用面积法来验证勾股定理吗?
如图所示,这是美国第20任总统加菲尔德证明勾股定理时所采用的图形,是用两个全等的直角三角形和一个等腰直角三角形拼出一个梯形.借助这个图形,你能用面积法来验证勾股定理吗?