题目内容
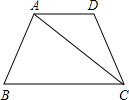
已知如图所示,在梯形ABCD中,AD∥BC,点M是AD)的中点.连接BM交AC于N.BM的延长线交CD的延长线于E.(1)求证:
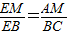 ;
;(2)若MN=1cm,BN=3cm,求线段EM的长.
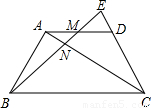
【答案】分析:(1)由于AD∥BC,易证得△MED∽△BEC;得 ;已知AM=MD,代换相等线段后即可得出本题要证的结论.
;已知AM=MD,代换相等线段后即可得出本题要证的结论.
(2)按照(1)的方法,可由AM∥BC,得出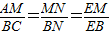 ,再联立(1)得出的比例关系式,可列出关于EM的方程,即可求得EM的长.
,再联立(1)得出的比例关系式,可列出关于EM的方程,即可求得EM的长.
解答:(1)证明:∵AD∥BC,
∴△MED∽△BEC,
∴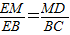 ,
,
又∵M是AD的中点,
∴AM=MD,
∴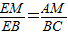 .
.
(2)解:∵△AMN∽△CBN,
∴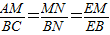 ,
,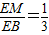
又∵EB=ME+MB,
MB=BN+NM=4cm,
∴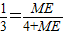
∴EM=2cm.
点评:此题主要考查了梯形的性质,以及相似三角形的判定和性质和解一元二次方程.
 ;已知AM=MD,代换相等线段后即可得出本题要证的结论.
;已知AM=MD,代换相等线段后即可得出本题要证的结论.(2)按照(1)的方法,可由AM∥BC,得出
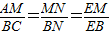 ,再联立(1)得出的比例关系式,可列出关于EM的方程,即可求得EM的长.
,再联立(1)得出的比例关系式,可列出关于EM的方程,即可求得EM的长.解答:(1)证明:∵AD∥BC,
∴△MED∽△BEC,
∴
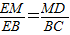 ,
,又∵M是AD的中点,
∴AM=MD,
∴
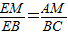 .
.(2)解:∵△AMN∽△CBN,
∴
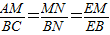 ,
,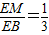
又∵EB=ME+MB,
MB=BN+NM=4cm,
∴
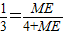
∴EM=2cm.
点评:此题主要考查了梯形的性质,以及相似三角形的判定和性质和解一元二次方程.

练习册系列答案
相关题目
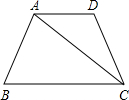 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC. D的延长线于E.
D的延长线于E.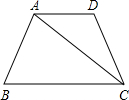 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.