题目内容
（2011•巴中）已知如图所示，在梯形ABCD中，AD∥BC，点M是AD）的中点．连接BM交AC于N．BM的延长线交C
D的延长线于E．
（1）求证：
=
；
（2）若MN=1cm，BN=3cm，求线段EM的长．
D的延长线于E．（1）求证：
| EM |
| EB |
| AM |
| BC |
（2）若MN=1cm，BN=3cm，求线段EM的长．
分析：（1）由于AD∥BC，易证得△MED∽△BEC；得
=
；已知AM=MD，代换相等线段后即可得出本题要证的结论．
（2）按照（1）的方法，可由AM∥BC，得出
=
=
，再联立（1）得出的比例关系式，可列出关于EM的方程，即可求得EM的长．
| EM |
| EB |
| MD |
| BC |
（2）按照（1）的方法，可由AM∥BC，得出
| AM |
| BC |
| MN |
| BN |
| EM |
| EB |
解答：（1）证明：∵AD∥BC，
∴△MED∽△BEC，
∴
=
，
又∵M是AD的中点，
∴AM=MD，
∴
=
．
（2）解：∵△AMN∽△CBN，
∴
=
=
，
=
又∵EB=ME+MB，
MB=BN+NM=4cm，
∴
=
∴EM=2cm．
∴△MED∽△BEC，
∴
| EM |
| EB |
| MD |
| BC |
又∵M是AD的中点，
∴AM=MD，
∴
| EM |
| EB |
| AM |
| BC |
（2）解：∵△AMN∽△CBN，
∴
| AM |
| BC |
| MN |
| BN |
| EM |
| EB |
| EM |
| EB |
| 1 |
| 3 |
又∵EB=ME+MB，
MB=BN+NM=4cm，
∴
| 1 |
| 3 |
| ME |
| 4+ME |
∴EM=2cm．
点评：此题主要考查了梯形的性质，以及相似三角形的判定和性质和解一元二次方程．
练习册系列答案
相关题目
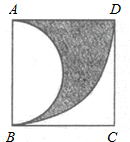（2011•巴中）已知如图所示，正方形ABCD的边长为1，以AB为直径作半圆，以点A为圆心，AD为半径画弧．那么图中阴影部分的面积为
（2011•巴中）已知如图所示，在平面直角坐标系中，四边形ABC0为梯形，BC∥A0，四个顶点坐标分别为A（4，0），B（1，4），C（0，4），O（0，O）．一动点P从O出发以每秒1个单位长度的速度沿OA的方向向A运动；同时，动点Q从A出发，以每秒2个单位长度的速度沿A→B→C的方向向C运动．两个动点若其中一个到达终点，另一个也随之停止．设其运动时间为t秒．