题目内容
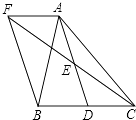
【题目】如图,在△ABC中,D是BC边上一点,E是AD的中点,过A作BC的平行线交CE的延长线F,且AF=BD,连结BF. 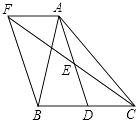
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论;
(3)当△ABC满足什么条件时,四边形AFBD为正方形?(写出条件即可,不要求证明)
【答案】
(1)证明:∵AF∥BC,
∴∠AFE=∠ECD.
∵E是AD的中点,
∴DE=AE,
在△AEF与△DEC中,
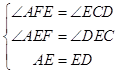 ,
,
∴△AEF≌△DEC(AAS),
∴AF=DC,
∵AF=BD,
∴BD=CD;
(2)答:四边形AFBD为矩形;
解:∵AF=BD,AF∥BD,
∴四边形AFBD为平行四边形,
∵AB=AC,BD=DC,
∴AD⊥BC,
∴∠BDA=90°,
∴四边形AFBD为矩形;
(3)解:AB=AC,且∠BAC=90°;
∵AB=AC,且∠BAC=90°,
∴∠ABC=45°,
∵AD⊥BC,
∴∠BAD=45°,
∴AD=DB,
∴四边形AFBD为正方形.
【解析】(1)证明△AEF≌△DEC可得AF=DC,再根据条件AF=BD可利用等量代换可得BD=CD;(2)首先判定四边形AFBD为平行四边形,再根据等腰三角形三线合一的性质可得AD⊥BC,进而可得四边形AFBD为矩形;(3)当AB=AC,且∠BAC=90°时,四边形AFBD为正方形,首先证明∠ABC=45°,∠BAD=45°,可得AD=BD,进而可得四边形AFBD为正方形.
【考点精析】关于本题考查的矩形的判定方法和正方形的判定方法,需要了解有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能得出正确答案.

【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间 (小时) | 频数 (人) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
频数分布直方图
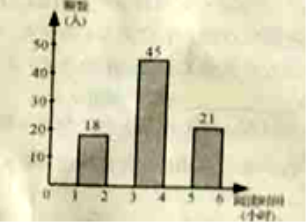
(1)填空:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)若该校由![]() 名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.
名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.