题目内容
阅读与证明:
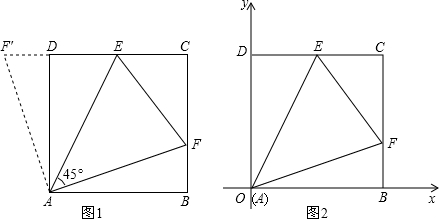
如图,已知正方形ABCD中,E、F分别是CD、BC上的点,且∠EAF=45°,求证:BF+DE=EF.

分析:证明一条线段等于另两条线段的和,常用“截长法”或“补短法”,将线段BF、DE放在同一直线上,构造出一条与BF+DE相等的线段.如图延长ED至点![]() ,使D
,使D![]() =BF,连接A
=BF,连接A![]() ,易证△ABF≌△AD
,易证△ABF≌△AD![]() ,进一步证明△AEF≌△AE
,进一步证明△AEF≌△AE![]() ,即可得结论.
,即可得结论.
(1)请你将下面的证明过程补充完整.
证明:延长ED至![]() ,使D
,使D![]() =BF,
=BF,
∵四边形ABCD是正方形
∴AB=AD,∠ABF=∠AD![]() =90°,
=90°,
∴△ABF≌△AD![]() (SAS)
(SAS)
应用与拓展:如图建立平面直角坐标系,使顶点A与坐标原点O重合,边OB、OD分别在x轴、y轴的正半轴上.

(2)设正方形边长OB为30,当E为CD中点时,试问F为BC的几等分点?并求此时F点的坐标;
(3)设正方形边长OB为30,当EF最短时,直接写出直线EF的解析式:________.
答案:
解析:
解析:
|
(1)证明:∴AF=A ∵∠ =∠DAB-∠EAF=45°, 又∵∠EAF=45°, ∴∠ ∴△AEF≌△AE ∴EF=E (2)解:设BF=a,则CF=30-a,EF=15+a 在Rt△CEF中 EC2+CF2=EF2 ∴152+(30-a)2=(15+a)2 ∴a=10(6分) ∴F为BC的三等分点(7分) ∴F(30,10)(8分) (3)y=-x+30 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目