题目内容
在一个不透明的盒子中,有三张除颜色外都相同的卡片,一张两面都是红色,一张两面都是黑色,另一张一面是红色,一面是黑色.
(1)从盒中任意抽出一张卡片,求至少有一面是红色的概率;
(2)小明和小颖玩抽卡片的游戏,规则如下:从盒中任意抽出一张卡片,放在桌子上,一面朝上,猜另一面的颜色.如果另一面的颜色与朝上一面的颜色相同,则小颖胜,反之,则小明胜.游戏共玩了5次,其中小明胜2次.因此,小明认为:在这个游戏中,自己获胜的概率一定是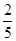 ,小颖获胜的概率一定是
,小颖获胜的概率一定是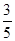 .而小颖则认为:假设抽出的卡片朝上一面是红色,则这张一定不可能是两面黑色的卡片,它或者是两面红,或者是两面不同,相同与不同机会各占一半,所以自己和小明获胜的概率都是
.而小颖则认为:假设抽出的卡片朝上一面是红色,则这张一定不可能是两面黑色的卡片,它或者是两面红,或者是两面不同,相同与不同机会各占一半,所以自己和小明获胜的概率都是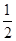 .请分别评述小明与小颖的观点是否正确,并判断这个游戏公平吗?简要说明理由.
.请分别评述小明与小颖的观点是否正确,并判断这个游戏公平吗?简要说明理由.
(1)从盒中任意抽出一张卡片,求至少有一面是红色的概率;
(2)小明和小颖玩抽卡片的游戏,规则如下:从盒中任意抽出一张卡片,放在桌子上,一面朝上,猜另一面的颜色.如果另一面的颜色与朝上一面的颜色相同,则小颖胜,反之,则小明胜.游戏共玩了5次,其中小明胜2次.因此,小明认为:在这个游戏中,自己获胜的概率一定是
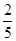 ,小颖获胜的概率一定是
,小颖获胜的概率一定是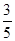 .而小颖则认为:假设抽出的卡片朝上一面是红色,则这张一定不可能是两面黑色的卡片,它或者是两面红,或者是两面不同,相同与不同机会各占一半,所以自己和小明获胜的概率都是
.而小颖则认为:假设抽出的卡片朝上一面是红色,则这张一定不可能是两面黑色的卡片,它或者是两面红,或者是两面不同,相同与不同机会各占一半,所以自己和小明获胜的概率都是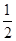 .请分别评述小明与小颖的观点是否正确,并判断这个游戏公平吗?简要说明理由.
.请分别评述小明与小颖的观点是否正确,并判断这个游戏公平吗?简要说明理由.(1)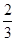 ;(2)都不正确
;(2)都不正确
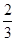 ;(2)都不正确
;(2)都不正确试题分析:(1)仔细分析题意根据概率公式求解即可.
(2)根据用频率估计概率需要建立在大量重复实验的基础上,同时结合概率公式即可作出判断.
(1)由题意得从盒中任意抽出一张卡片,至少有一面是红色的概率为
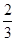 ;
;(2)小明与小颖的观点都不正确.
小明的观点:用频率估计概率需要建立在大量重复实验的基础上,本题游戏只进行了五次,因此不能用各人获胜的频率去估计概率,所以小明的观点不正确.
小颖的观点:三张牌中有两张两面相同,一张两面不同,每张牌被抽到的可能性相同,因此两面相同的概率应为
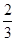 ,两面不同的概率为
,两面不同的概率为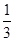 ,小颖的观点也不正确.游戏是不公平的.
,小颖的观点也不正确.游戏是不公平的.点评:解题的关键是熟练掌握概率公式:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率
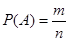 .
.
练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目





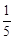
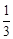


 、乙立方体朝上一面朝上的数字为
、乙立方体朝上一面朝上的数字为 ,这样就确定点P的一个坐标(
,这样就确定点P的一个坐标( ),那么点P落在双曲线
),那么点P落在双曲线 上的概率为( )
上的概率为( )



 ,乙组数据的方差
,乙组数据的方差 ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定