题目内容
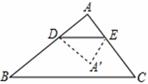
如图1,已知有一张三角形纸片ABC的一边AB=10,若D为AB边上的点,过点D作DE//BC交AC于点E,分别过点D、E作DF⊥BC,EG⊥BC,垂足分别为点F、点G,把三角形纸片ABC分别沿DE、DF、EG按图1方式折叠,点A、B、C分别落在A´、B´、C´处.若A´、B´、C´在矩形DFGE内或者其边上,且互不重合,此时我们称△A´B´C´(即图中阴影部分)为“重叠三角形”.
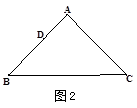
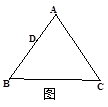
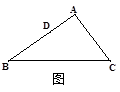
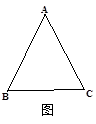
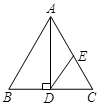
(1)实验操作:当AD=4时,①若∠A=90°,AB=AC,请在图2中画出“重叠三角形”,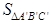 = ;
= ;
②若AB=AC,BC=12,如图3,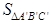 = ;③若∠B=30°,∠C=45°,如图4,
= ;③若∠B=30°,∠C=45°,如图4,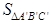 = ;
= ;
(2)实验探究:若△ABC为等边三角形(如图5),设AD的长为m,若重叠三角形A´B´C´存在,试用含m的代数式表示重叠三角形A´B´C´的面积,并写出m的取值范围.

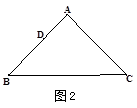
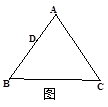
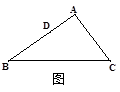
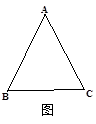
(1)实验操作:当AD=4时,①若∠A=90°,AB=AC,请在图2中画出“重叠三角形”,
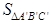 = ;
= ; ②若AB=AC,BC=12,如图3,
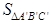 = ;③若∠B=30°,∠C=45°,如图4,
= ;③若∠B=30°,∠C=45°,如图4,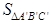 = ;
= ; (2)实验探究:若△ABC为等边三角形(如图5),设AD的长为m,若重叠三角形A´B´C´存在,试用含m的代数式表示重叠三角形A´B´C´的面积,并写出m的取值范围.
(1)①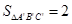 ;②
;②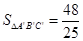 ;③
;③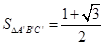 ;(2)
;(2)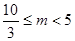
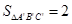 ;②
;②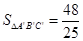 ;③
;③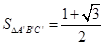 ;(2)
;(2)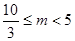
试题分析:(1)仔细分析题意,根据“重叠三角形”的定义结合三角形的面积公式求解即可;
(2)由AD=m可得A´D=AD=m,B´D=BD=10-m,则可得A´B´=10-2m,先证得△A´B´C´为等边三角形,根据三角形的面积公式可表示出△A´B´C´的面积,由B´C´
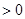 结合B´C´
结合B´C´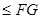 即可得到关于m的不等式组,从而求得结果.
即可得到关于m的不等式组,从而求得结果.(1)由题意得①
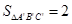 ;②
;②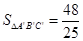 ;③
;③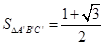
(2)
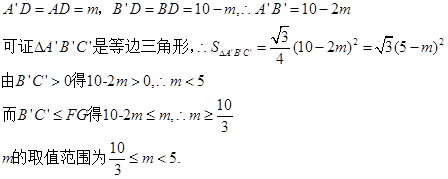
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目
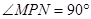 ,PM=3,PN=4,,那么矩形纸片ABCD的面积为 .
,PM=3,PN=4,,那么矩形纸片ABCD的面积为 .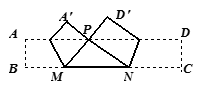
 AP。
AP。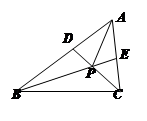
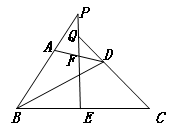
 、
、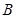 是方格纸的两个格点(即正方形的顶点),在这个
是方格纸的两个格点(即正方形的顶点),在这个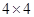 的方格纸中,找出格点
的方格纸中,找出格点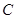 ,使
,使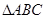 是等腰三角形,这样的点
是等腰三角形,这样的点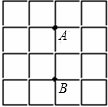
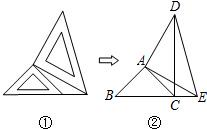
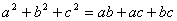 ,则△ABC是 三角形。
,则△ABC是 三角形。