题目内容
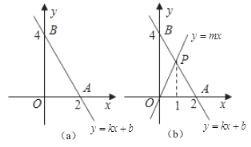
【题目】已知一次函数![]() (k,b为常数,且
(k,b为常数,且![]() )的图像如图(a)所示,
)的图像如图(a)所示,
(1)方程![]() 的解为 ,不等式
的解为 ,不等式![]() 的解集是________.
的解集是________.
(2)如图(b)所示,正比例函数![]() (m为常数,且
(m为常数,且![]() )与一次函数
)与一次函数![]() 相交于点P,则不等式组
相交于点P,则不等式组![]() 的解集为________.
的解集为________.
(3)在(2)的条件下,比较mx与![]() 的大小(直接写出结果).
的大小(直接写出结果).
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
(1)由图象可知:当![]() 时,y=0,即可求出方程
时,y=0,即可求出方程![]() 的解,然后根据图象可知当x=0时,y=4,y随x增大而减小,从而求出不等式
的解,然后根据图象可知当x=0时,y=4,y随x增大而减小,从而求出不等式![]() 的解集;
的解集;
(2)根据图象分别求出mx>0的解集和![]() >0的解集即可得出结论;
>0的解集即可得出结论;
(3)由图象可知:在交点P左侧时,正比例函数![]() 的函数值比一次函数
的函数值比一次函数![]() 函数值小;在交点P处,正比例函数
函数值小;在交点P处,正比例函数![]() 的函数值和一次函数
的函数值和一次函数![]() 函数值相等;在交点P右侧时,正比例函数
函数值相等;在交点P右侧时,正比例函数![]() 的函数值比一次函数
的函数值比一次函数![]() 函数值大,即可得出结论.
函数值大,即可得出结论.
解:(1)由图象可知:当![]() 时,y=0
时,y=0
∴方程![]() 的解为
的解为![]()
由图象可知:当x=0时,y=4,y随x增大而减小
∴当![]() 时,
时,![]()
![]() 的解集是
的解集是![]()
故答案为:![]() ;
;![]() ;
;
(2)由图象可知:正比例函数![]() 中,当x=0时,y=0,y随x的增大而增大
中,当x=0时,y=0,y随x的增大而增大
∴当x>0时,![]() >0
>0
∴mx>0的解集为x>0
一次函数![]() 中,当x=2时,y=0,y随x增大而减小
中,当x=2时,y=0,y随x增大而减小
∴当x<2时,![]() >0,
>0,
∴![]() >0的解集为x<2
>0的解集为x<2
∴不等式组![]() 的解集为
的解集为![]() .
.
故答案为:![]() .
.
(3)由图象可知:在交点P左侧时,正比例函数![]() 的函数值比一次函数
的函数值比一次函数![]() 函数值小;在交点P处,正比例函数
函数值小;在交点P处,正比例函数![]() 的函数值和一次函数
的函数值和一次函数![]() 函数值相等;在交点P右侧时,正比例函数
函数值相等;在交点P右侧时,正比例函数![]() 的函数值比一次函数
的函数值比一次函数![]() 函数值大.
函数值大.
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.

【题目】某市扶贫办在精准扶贫工作中,组织30辆汽车装运花椒、核桃、甘蓝向外地销售.按计划30辆车都要装运,每辆汽车只能装运同一种产品,且必须装满,根据下表提供的信息,解答以下问题:
产品名称 | 核桃 | 花椒 | 甘蓝 |
每辆汽车运载量(吨) | 10 | 6 | 4 |
每吨土特产利润(万元) | 0.7 | 0.8 | 0.5 |
若装运核桃的汽车为x辆,装运甘蓝的车辆数是装运核桃车辆数的2倍多1,假设30辆车装运的三种产品的总利润为y万元.
(1)求y与x之间的函数关系式;
(2)若装花椒的汽车不超过8辆,求总利润最大时,装运各种产品的车辆数及总利润最大值.
【题目】今年是“五四”运动![]() 周年,为进一步弘扬“爱国、进步、民主、科学”的五四精神,引领广大团员青年坚定理想信念,某市团委、少先队共同举办纪念“五四运动
周年,为进一步弘扬“爱国、进步、民主、科学”的五四精神,引领广大团员青年坚定理想信念,某市团委、少先队共同举办纪念“五四运动![]() 周年”读书演讲比赛,甲同学代表学校参加演讲比赛,
周年”读书演讲比赛,甲同学代表学校参加演讲比赛,![]() 位评委给该同学的打分(单位:分)情况如下表:
位评委给该同学的打分(单位:分)情况如下表:
评委 | 评委1 | 评委2 | 评委3 | 评委4 | 评委5 | 评委6 | 评委7 |
打分 |
|
|
|
|
|
|
|
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数.