Question

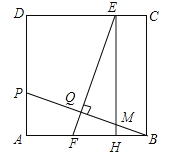
【题目】如图，在正方形ABCD中，点P在AD上，且不与A、D重合，BP的垂直平分线分别交CD、AB于E、F两点，垂足为Q，过E作EH⊥AB于H．

（1）求证：HF=AP；

（2）若正方形ABCD的边长为12，AP=4，求线段EQ的长．

Answer 1

【答案】（1）证明见试题解析；（2）．

【解析】

试题分析：（1）由EQ⊥BO，EH⊥AB得到∠EQN=∠BHM=90°，由∠EMQ=∠BMH得到△EMQ∽△BMH，故∠QEM=∠HBM．由ASA定理得到△APB≌△HFE，故可得出结论；

（2）根据勾股定理求出BP的长，由EF是BP的垂直平分线可知BQ=BP，再由锐角三角函数的定义得出QF=BQ的长，由（1）知，△APB≌△HFE，故EF=BP=，再由EQ=EF﹣QF即可得出结论．

试题解析：（1）∵EQ⊥BO，EH⊥AB，∴∠EQN=∠BHM=90°，∵∠EMQ=∠BMH，∴△EMQ∽△BMH，∴∠QEM=∠HBM，在Rt△APB与Rt△HFE中，∵∠QEM=∠HBM，∠PAB=∠FHE，AB=EH，∴△APB≌△HFE，∴HF=AP；

（2）由勾股定理得，BP===4，∵EF是BP的垂直平分线，∴BQ=BP=，∴QF=BQtan∠FBQ=BQtan∠ABP==，由（1）知，△APB≌△HFE，∴EF=BP=，∴EQ=EF﹣QF==．