Question

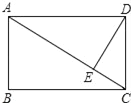
【题目】如图，在矩形ABCD中，DE⊥AC于E，cos∠ADE=，AB=3.

（1）求AD的值；

（2）直接写出S△DEC的值是_____．

Answer 1

【答案】（1）4；（2）.

【解析】试题分析：（1）首先证明∠ADE=∠ACD，可得cos∠ACD=cos∠ADE==，由此即可求出AC，再利用勾股定理求出AD即可；

（2）根据cos∠DCE==，求出EC，再利用勾股定理求出DE，即可解决问题；

试题解析：解：（1）∵四边形ABCD是矩形，∴AB=CD=3，∠ADC=90°．∵DE⊥AC，∴∠ADE+∠CDE=90°，∠CDE+∠DCE=90°，∴∠ADE=∠ACD，∴cos∠ACD=cos∠ADE==，∴AC=5，AD==4．

（2）∵cos∠DCE==，∴CE=，DE==，∴S△DEC=×DE×EC=××=

故答案为： ．