题目内容
已知△ABC与△DEF相似且面积比为4：25，则△ABC与△DEF的相似比为（ ）
分析：根据相似三角形的面积的比等于相似比的平方，可直接得出结果．
解答：解：∵△ABC∽△DEF，
∴△ABC与△DEF的面积比等于相似比的平方，
又∵S△ABC：S△DEF=4：25=（2：5）2，
∴△ABC与△DEF的相似比为2：5．
故选D．
∴△ABC与△DEF的面积比等于相似比的平方，
又∵S△ABC：S△DEF=4：25=（2：5）2，
∴△ABC与△DEF的相似比为2：5．
故选D．
点评：本题考查相似三角形的性质．利用相似三角形的性质时，要注意相似比的顺序，同时也不能忽视面积比与相似比的关系．相似比是联系周长、面积、对应线段等的媒介，也是相似三角形计算中常用的一个比值．
练习册系列答案
相关题目
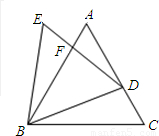
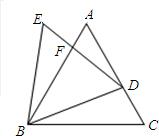如图，已知△ABC与△BDE都是等边三角形，点D在边AC上（不与A、C重合），DE与AB相交于点F．
如图，已知△ABC与△BDE都是等边三角形，点D在边AC上（不与A、C重合），DE与AB相交于点F．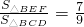
？
？