题目内容
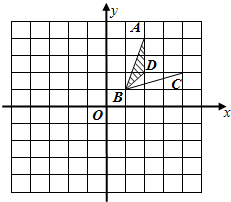 在如图所示的网格中,每个小方格的边长都是1.
在如图所示的网格中,每个小方格的边长都是1.(1)分别作出四边形ABCD关于y轴、原点的对称图形;
(2)以原点O为中心,将△ABD顺时针旋转90°,试画出旋转后的图形,并求旋转过程中△ABD扫过图形的面积.
分析:(1)根据关于y轴对称及关于原点对称的点的性质,分别作出A、B、C和D四个顶点关于y轴及原点的对称点,然后顺次连接各对应点即可;
(2)先画出△ABD顺时针旋转90°后得到的图形,△ABD扫过图形的面积即是线段AB所扫过的扇环面积与△ABD的面积之和.
(2)先画出△ABD顺时针旋转90°后得到的图形,△ABD扫过图形的面积即是线段AB所扫过的扇环面积与△ABD的面积之和.
解答:解:(1)所画图形如下图所示,
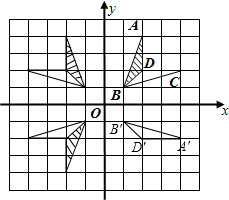
(2)如上图所示,△A′B′D′即为△ABD顺时针旋转90°后得到的图形,
在旋转过程中可知:△ABD扫过图形的面积即是线段AB所扫过的扇环面积(S1)与△ABD的面积(S2)之和(S),
则有:S=S1+S2=[
π×OA2-
π×OB2]+
×AD×1
=[
π×(22+42)-
π×(12+12)]+
×2×1
=
+1.

(2)如上图所示,△A′B′D′即为△ABD顺时针旋转90°后得到的图形,
在旋转过程中可知:△ABD扫过图形的面积即是线段AB所扫过的扇环面积(S1)与△ABD的面积(S2)之和(S),
则有:S=S1+S2=[
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
=[
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
=
| 9π |
| 2 |
点评:此题主要考查了关于坐标轴以及原点对称的图形作法和不规则图形的面积求法,得出对应点的坐标及将不规则图形分为几个规则的图形来求面积是解决问题的关键.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

 在如图所示的网格中,每个小正方形边长为1.
在如图所示的网格中,每个小正方形边长为1.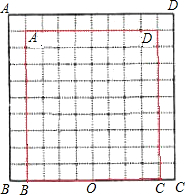 在如图所示的网格中,以BC的中点O为位似中心,把矩形ABCD缩小为原来的
在如图所示的网格中,以BC的中点O为位似中心,把矩形ABCD缩小为原来的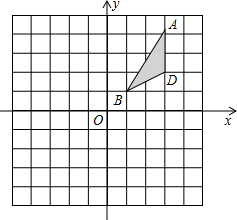 在如图所示的网格中,每个小方格的边长都是1.
在如图所示的网格中,每个小方格的边长都是1.