题目内容
【题目】已知抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)的顶点为M,经过原点O且与x轴另一交点为A.
(1)求点A的坐标;
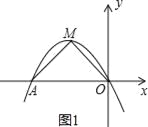
(2)若△AMO为等腰直角三角形,求抛物线C1的解析式;
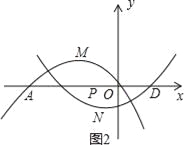
(3)现将抛物线C1绕着点P(m,0)旋转180°后得到抛物线C2,若抛物线C2的顶点为N,当b=1,且顶点N在抛物线C1上时,求m的值.
【答案】(1)(﹣4,0);(2)y=﹣![]() x2﹣2x;(3)m=﹣2+
x2﹣2x;(3)m=﹣2+![]() 或﹣2﹣
或﹣2﹣![]() .
.
【解析】试题分析:(1)、由抛物线经过原点可知当x=0时,y=0,由此可得关于x的一元二次方程,解方程即可求出抛物线x轴另一交点坐标;(2)、由△AMO为等腰直角三角形,抛物线的顶点为M,可求出b的值,再把原点坐标(0,0)代入求出a的值,即可求出抛物线C1的解析式;(3)、由b=1,易求线抛物线C1的解析式,设N(n,﹣1),再由点P(m,0)可求出n和m的关系,当顶点N在抛物线C1上可把N的坐标代入抛物线即可求出m的值.
试题解析:(1)、∵抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)经过原点O, ∴0=4a+b,
∴当ax2+4ax+4a+b=0时,则ax2+4ax=0, 解得:x=0或﹣4,∴抛物线与x轴另一交点A坐标是(﹣4,0);
(2)、∵抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b(a≠0,b>0),(如图1) ∴顶点M坐标为(﹣2,b),
∵△AMO为等腰直角三角形, ∴b=2, ∵抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b过原点,
∴a(0+2)2+2=0, 解得:a=﹣![]() , ∴抛物线C1:y=﹣
, ∴抛物线C1:y=﹣![]() x2﹣2x;
x2﹣2x;
(3)、∵b=1,抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b过原点,(如图2) ∴a=﹣![]() ,
,
∴y=﹣![]() (x+2)2+1=﹣
(x+2)2+1=﹣![]() x2﹣x, 设N(n,﹣1),又因为点P(m,0), ∴n﹣m=m+2,
x2﹣x, 设N(n,﹣1),又因为点P(m,0), ∴n﹣m=m+2,
∴n=2m+2 即点N的坐标是(2m+2,﹣1), ∵顶点N在抛物线C1上, ∴﹣1=﹣![]() (2m+2+2)2+1,
(2m+2+2)2+1,
解得:m=﹣2+![]() 或﹣2﹣
或﹣2﹣![]() .
.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案