题目内容
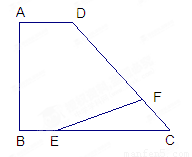
已知:如图在直角梯形COAB中,OC∥AB,以O为原点建立平面直角坐标系,A、B、C三点的坐标分别为A(8,0),B(8,11),C(0,5),点D为线段BC中点,已知D点的横坐标为4,动点P从点O出发,以每秒1个单位的速度,沿折线OABD的路线移动,至点D停止,设移动的时间为t秒
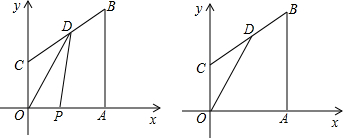
(1)求直线BC的解析式;
(2)若动点P在线段OA上移动,当t为何值时,四边形OPDC的面积是梯形COAB面积的 ?
?
(3)动点P从点O出发,沿折线OABD的路线移动过程中,设△OPD面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
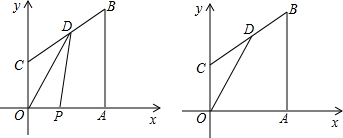 解:(1)设直线BC的解析式为y=kx+b,直线过B(8,11),C(0,5),
解:(1)设直线BC的解析式为y=kx+b,直线过B(8,11),C(0,5),∴
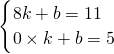 ,
,解得
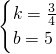 ,
,解析式为y=
 x+5;
x+5;(2)∵点D为线段BC的中点,
∴D(4,8)
由题意得
 ×5×4+
×5×4+ ×8t=
×8t= ×
× ×8×(5+11),
×8×(5+11),解得t=
 (s);
(s);(3)当P在OA上时,S=
 ×t×8=4t (0<t≤8)
×t×8=4t (0<t≤8)当P在AB上时,S=
 (4+10)×8-
(4+10)×8- ×4×4-
×4×4- ×8×(t-8)-
×8×(t-8)- (18-t)×4,
(18-t)×4,S=-2t+44 (8<t≤18)
当P在BD上时,S=S梯形OCAB-S三角形OCD-S三角形OPA-S三角形ABP
=56-8-4[10-
 (t-18)]-5(t-18)
(t-18)]-5(t-18)
=-
 t+
t+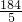 .(18<t<23)
.(18<t<23)当P在OD上时,S=0(23≤t≤23+
 );
);答:(1)解析式为y=
 t+4;
t+4;(2)当t=
 (s)时,四边形OPDC的面积是梯形COAB面积的
(s)时,四边形OPDC的面积是梯形COAB面积的 ;
;(3)分别是S=
 ×t×8=4t (0<t≤8),S=-2t+44 (8<t≤18),S=
×t×8=4t (0<t≤8),S=-2t+44 (8<t≤18),S=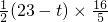 =-
=- t+
t+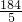 .(18<t<23);S=0(23≤t≤23+
.(18<t<23);S=0(23≤t≤23+ ).
).分析:(1)题目给出了B、C点的坐标,可设出直线BC的解析式,应用待定系数法求出解析式即可;
(2)可根据四边形OPDC的面积是梯形COAB面积的
 列出方程并解出方程即可;
列出方程并解出方程即可;(3)要根据P的位置在不同边的具体情况利用相关的知识写出函数关系式及取值范围.
点评:本题考查了一次函数的综合运用;做题时要认真理解题意,找出等量关系,而分类讨论是正确解答本题的关键.

练习册系列答案
相关题目

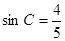 ,
,