题目内容
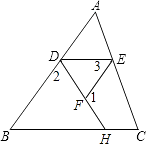
【题目】如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O. 
(1)求证:OB=OC.
(2)若∠ABC=65°,求∠COD的度数.
【答案】
(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BD、CE是△ABC的两条高线,
∴∠BEC=∠BDC=90°,
在△BEC和△CDB中,
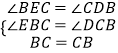 ,
,
∴△BEC≌△CDB,
∴∠DBC=∠ECB,BE=CD,
在△BOE和△COD中,
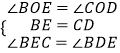 ,
,
∴△BOE≌△COD,
∴OB=OC
(2)解:∵∠ABC=65°,AB=AC,
∴∠A=180°﹣2×65°=50°,
∴∠COD=∠A=50°
【解析】(1)首先根据等腰三角形的性质得到∠ABC=∠ACB,然后利用高线的定义得到∠ECB=∠DBC,从而得证;(2)首先求出∠A的度数,进而求出∠COD的度数.
【考点精析】本题主要考查了等腰三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.

练习册系列答案
相关题目