题目内容
【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
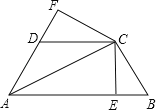
(1)求证:△BCE≌△DCF;
(2)若AB=15,AD=7,求BE的长.
【答案】(1)见解析;(2)BE=4.
【解析】
(1)由角平分线定理可得CE=CF,利用HL即可判定Rt△BCE≌Rt△DCF;
(2)首先利用HL证明Rt△AEC≌Rt△AFC,得到AE=AF,然后由Rt△BCE≌Rt△DCF得BE=DF,最后根据AE+BE=AF+BE=AD+2BE即可得出答案.
证明:(1)∵AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,
∴CE=CF,∠CEB=∠CFD=90°,
即△CBE和△CFD,△ACE和△ACF都是直角三角形.
在Rt△BCE和Rt△DCF中,
∵CE=CF,BC=CD,
∴Rt△BCE≌Rt△DCF(HL).
(2)在Rt△AEC和Rt△AFC中,
∵AC=AC,CE=CF,
∴Rt△AEC≌Rt△AFC(HL),
∴AE=AF.
由(1)知,Rt△BCE≌Rt△DCF,
∴BE=DF.
∵AB=15,AD=7,
∴AE+BE=15=AF+BE,
∴AD+DF+BE=15,
∴2BE=15-7=8,
∴BE=4.

练习册系列答案
相关题目






