题目内容
【题目】已知一次函数 
的图象与 
、 
轴分别交于点 
、 
，直线 
经过 
上的三分之一点 
，且交 轴的负半轴于点 
，如果 
，求直线 的解析式．
【答案】（1）
点的坐标为 
或 
（2）
或 
．
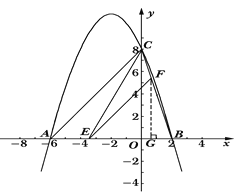
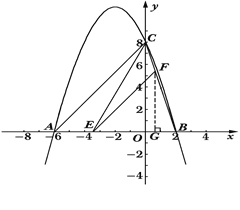
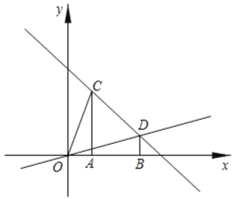
【解析】试题分析: 根据y＝
与y轴,x轴的交点分别为A,B,得出A,B两点的坐标,再根据D为OA上的三分之一点,得出D点的坐标,进而得出C点的坐标,即可求出解析式．
试题解析:因为直线y＝与y轴,x轴的交点分别为A,B,所以两点坐标分别为A（0,3）,B（2,0）,所以OA=3,OB=2,所以S△AOB＝
OAOB＝3,
因为D为OA上的三分之一点,所以D点的坐标为（0,1）或（0,2）,
因为S△AOB＝S△DOC＝OCOD＝3,所以当OD=1时,OC=6,当OD=2时,OC=3,
因为点C在x轴的负半轴上,所以C点的坐标为（-6,0）或（-3,0）,
所以直线CD的解析式为y＝
或
.
练习册系列答案
相关题目
